Lecture01
Definition – Decision Support (决策支持)
This term is used often and in a variety of contexts related to decision making.
Multidisciplinary:
- Artificial Intelligence,
- Operations Research,
- Decision Theory,
- Decision Analysis,
- Statistics,…
Definition – Systems
Degree of dependence of systems on the environment (系统对环境的依赖程度)
- Closed systems are totally independent (封闭系统)
- Open systems dependent on their environment (开放系统)
Evaluations of systems (系统评估)
System effectiveness: the degree to which goals are achieved, i.e. result, output (系统有效性)
System efficiency: a measure of the use of inputs (or resources) to achieve output, e.g., speed (系统效率)
Definition –Global Optimisation
Global optimisation is the task of finding the absolutely best set of admissible conditions to achieve your objective, formulated in mathematical terms. (全局优化定义:在数学条件下寻找达到目标的最佳)
Fundamental problem of optimisation is to arrive at the best possible (optimal) decision/solution in any given set of circumstances. (优化的基本问题)
In most cases “the best” (optimal) is unattainable (难以达到最优)
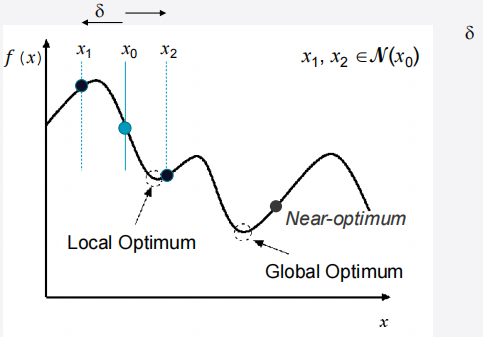
Global vs Local Optimum
- Global Optimum: better than all other solutions (best)
- Local Optimum: better than all solutions in a certain neighborhood, N
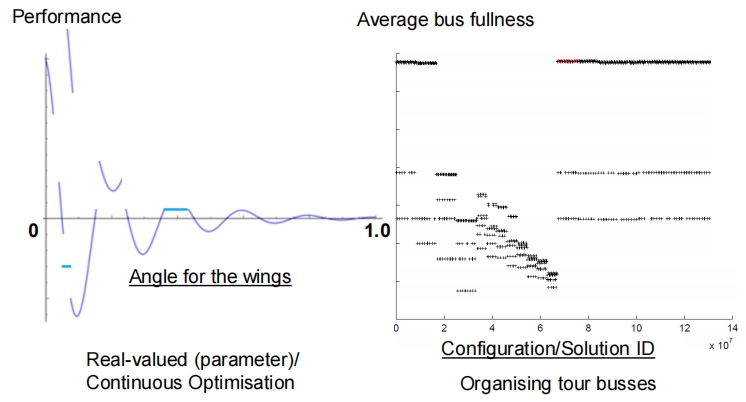
Search in Continuous vs Discrete Space
Definition – Problem and Problem Instance
- Problem refers to the high level question or optimisation issue to be solved.
- An instance of this problem is the concrete expression, which represents the input for a decision or optimisation problem.
- Example: Optimal assignment of groups to busses (minimising the number of busses) is an optimisation (minimisation) problem
- Optimal assignment of 3 groups of 10, 15, 43 to busses, each with 45 seats and company having 10 busses at max is an instance of this problem
- Optimal assignment of 5 groups of 19, 25, 30, 30, 45 to busses, each with 60 seats and company having 10 busses at max is another instance of this problem
Analysis of Algorithms 101: Problem Classes
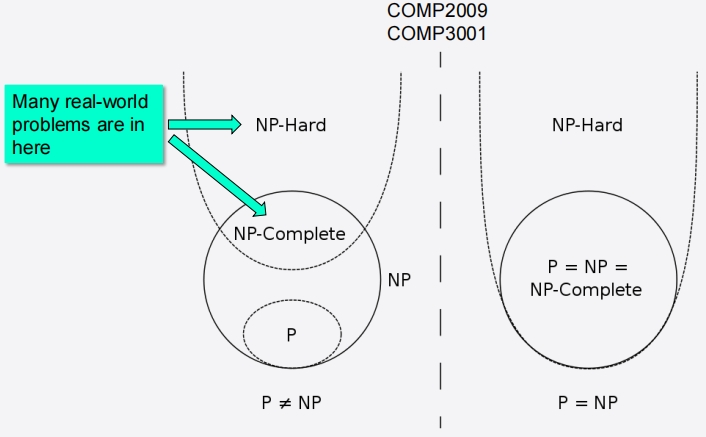
Combinatorial Optimisation Problems
Optimisation/Search Methods
- Optimisation methods can be broadly classified as:
- Exact/Exhaustive/Systematic Methods
- E.g., Dynamic Programming, Branch&Bound, Constraint Satisfaction, Math programming…
- Inexact/Approximate/Local Search Methods
- E.g., heuristics, metaheuristics, hyper-heuristics,…
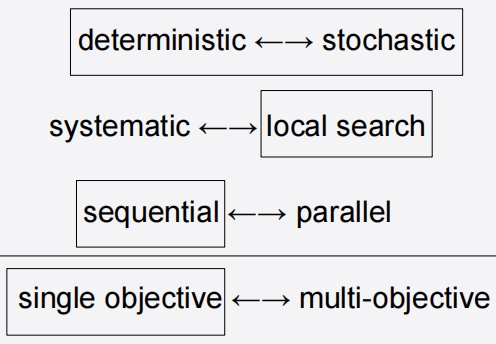
Search Paradigms I
Single point (trajectory) based search vs. Multi-point (population) based search (单点搜索是指在解空间中沿着一条路径(或轨迹)进行搜索,而多点搜索则是在解空间中同时考虑多个点(或一组点,也称为种群)进行搜索)
Perturbative (微扰性搜索:这是一种搜索策略,它通过对当前解进行小的、随机的改变(或微扰)来生成新的解。这种方法通常用于寻找全局最优解,特别是在解空间中存在许多局部最优解的情况下)
- complete solutions
Constructive (构造性搜索:这是一种搜索策略,它通过逐步构建解的部分来生成完全解。这种方法通常用于解决组合优化问题,如旅行商问题或者图着色问题)
- partial solutions (在搜索过程中,部分解通常被用作中间步骤,以帮助找到完全解)
Search Paradigms II
Example Optimisation Techniques I
Exact/Exhaustive/Deterministic Systematic Methods
- Dynamic Programming (动态规划:将问题分解为更小的子问题,并将子问题的解存储起来)
- Branch & Bound (分支定界:树中搜索最优解)
- Constraint Satisfaction (约束满足:八皇后)
- Math programming (数学规划)
- ILP (整数线性规划)
- MILP (混合整数线性规划)
Limitations:
- Only work if the problem is structured – in many cases for small problem instances (只有在问题是结构化的情况下才有效)
- Quite often used to solve sub-problems (往往被用来解决子问题)
Heuristic Search Methods ( is a rule of thumb method)
- A heuristic is a problem dependent search method which seeks good, i.e. near-optimal solutions, at a reasonable cost (e.g. speed) without being able to guarantee optimality.
- Good for solving ill-structured problems, or complex well-structured problems (large-scale combinatorial problems that have many potential solutions to explore) (启发式方法特别适合解决结构不良的问题,或者复杂的结构良好的问题)
Deterministic vs Stochastic Heuristic Search
- Deterministic heuristic search algorithms provide the same solution when run on the given problem instance regardless of how many times. (确定性启发式搜索算法在给定问题实例上运行时,无论运行多少次,都会提供相同的解决方案)
- Stochastic algorithms contain a random component and may return a different solution at each time they are run on the same instance (可能在每次在同一实例上运行时返回不同的解决方案)
- Multiple trials/runs should be performed for the experiments/simulations
- Being able to repeat/replicate those multiple trials/runs in the experiments/simulations is crucial in science, and
- This also enables average performance comparison of different stochastic heuristic search algorithms applying statistical tests
Lecture02
1. Representation
Representation (Encoding of a Solution) – Characteristics
Completeness: all solutions associated with the problem must be represented. (完整性:所有可能的解被编码,确保不错过最优解)
Connexity: a search path must exist between any two solutions of the search space. Any solution of the search space, especially the global optimum solution, can be attained. (连通性:从搜索空间中的任何一个解出发,理论上都能通过一系列操作到达任何其他解,特别是全局最优解)
Efficiency: The representation must be easy/fast to manipulate by the search operators.(效率:快速且容易地处理,减少计算成本)
Representation Type
- Binary encoding
- Permutation encoding (旅行商问题(TSP),其中城市的访问顺序决定了总旅行距离)
- Integer encoding (资源分配问题)
- Value Encoding
- Nonlinear Encoding(复杂的结构,如树、图等)
Boolean Satisfiability(SAT) Problem
Given n Boolean literals/variables, what is the number of possible configurations (search space size)? –>(2^n)
(每个变量有两种可能的状态:真(True)或假(False),总的配置数(搜索空间大小)是所有可能的变量状态组合)
2. Neighbourhoods
Definition
A neighbourhood of a solution x is a set of solutions that can be reached from x by a simple operator (move operator/heuristic)(一个解的邻域包含了所有与之相似且通过某种小幅度修改能够直接到达的解)
Example Neighbourhood for Binary Representation
Bit-flip operator: flips a bit in a given solution
Hamming Distance between two bit strings (vectors) of equal length is the number of positions at which the corresponding symbols differ. E.g., HD(011,010)=1, HD(0101,0010)=3 (汉明距离是两个等长二进制向量(字符串)之间的差异度量,即在相同位置上数值不同的位数。它是一种衡量两个解相似度的指标)
If the binary string is of size n, then the neighbourhood size is n.
Example: 1 0 1 0 0 0 1 1 → 0 0 1 0 0 0 1 1
Neighbourhood size: 8, Hamming distance: 1
Example Neighbourhood for Integer/Value Representation

计算公式:如果解的大小是n(即解中的元素数量),并且字母表的大小是k(可选用的不同值的数量),那么可能的邻域大小是(k−1)n。这是因为每个元素都可以被替换为字母表中的k−1个其他值(当前值除外),且解中有n个这样的元素。
Example Neighbourhood for Permutation Representation
- Adjacent pairwise interchange: swap adjacent entries in the permutation(相邻对换)
- If permutation is of size n, then the neighbourhood size is n-1
- Example: 5 1 4 3 2 → 1 5 4 3 2
- Insertion operator: take an entry in the permutation and insert it in another position
- Neighbourhood size: n(n-1) (每个元素有n−1个可能的新位置)
- Example: 5 1 4 3 2 → 1 4 5 3 2
- Exchange operator: arbitrarily selected two entries are swapped(任意交换)
- Example: 5 4 3 1 2 → 1 4 3 5 2
- Inversion operator: select two arbitrary entries and invert the sequence in between them(倒置)
- Example: 1 4 5 3 2 → 1 3 5 4 2
3. Evaluation/Objective Function
Evaluation Function
Also referred to as objective, cost, fitness, penalty, etc.
- Indicates the quality of a given solution, distinguishing between better and worse solutions
Serves as a major link between the algorithm and the problem being solved
- provides an important feedback for the search process
Many types: (non)separable, uni/multi-modal, single/multi objective, etc.
Evaluation functions could be computationally expensive
Exact vs. approximate
- Common approaches to constructing approximate models: polynomials, regression, SVMs, etc.
- Constructing a globally valid approximate model remains difficult, and so beneficial to selectively use the original evaluation function together with the approximate model
MAX-SAT Problem – Evaluation function

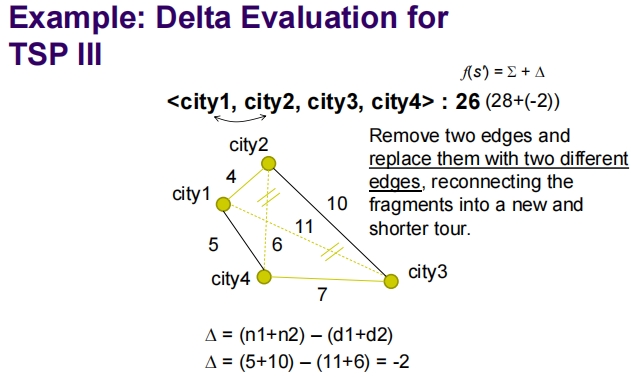
TSP – Evaluation function

Evaluation Function – Delta (Incremental) Evaluation

4. Hill Climbing Algorithms
Pseudocode of a Generic Hill Climbing Algorithm
Pick an initial starting point (current state) in the search space
Repeat
- Consider the neighbors of the current state (考虑邻域)
- Compare new point(s) in the neighborhood of the current state with the current state using an evaluation function and choose a new point with the best quality (among them) and move to that state (使用评价函数比较并选择)
Until there is no more improvement or when a predefined number of iterations is reached (邻域里没有比当前状态更好的)
Return the current state as the solution state
Simple Hill Climbing Heuristics
- Simple Hill Climbing examining neighbours:
- Best improvement (steepest descent/ascent) (每一步都寻找当前解的所有邻居,并选择改进最大的那个邻居作为下一个解)
- First improvement (next descent/ascent) (找到任何比当前解更好的邻居后立即移动)
- Stochastic Hill Climbing (randomly choose neighbours)
- Random selection/random mutation hill climbing (随机选择当前解的一个邻居来决定的,而不是基于评价函数的改进)
- Random-restart (shotgun) hill climbing is built on top of hill climbing and operates by changing the starting solution for the hill climbing, randomly and returning the best (算法从一个随机选择的初始解开始,执行爬山搜索,如果陷入局部最优解或达到某个终止条件,则重新开始搜索,选择另一个随机初始解)
Davis’s (Bit) Hill-climbing
生成序列,然后根据序列翻转顺序bit,产生优解就在优解基础上继续翻转接下来的bit

Hill Climbing Algorithms – When to Stop
- If the target objective is known (e.g., minimum value for f2 is known which is 0), then the search can be stopped when that target objective value is achieved. (一旦达到这个目标值,搜索可以立即停止)
- Hill climbing could be applied repeatedly until a termination criterion is satisfied (e.g. maximum number of evaluations is exceeded which is a factor of the string length)
- Note that there is no point applying Best Improvement, Next Improvement and Davis’s (Bit) Hill Climbing if there is no improvement after any single pass over a solution.
- Random Mutation Hill Climbing requires consideration.
Strengths and Weaknesses of Hill Climbing
Strengths of Hill Climbing
- Very easy to implement, requiring: a representation, an evaluation function and a measure
Weaknesses of Hill Climbing
- Local Optimum (局部最优可能全局最优很远)
- Plateau (neutral space/shoulder)(当前状态的所有邻居状态都与当前状态一样好(评价函数值相同),则称该区域为高原)(在高原上,爬山算法可能会进行随机行走,因为它无法通过局部搜索找到改进的方向)
- Ridge/valley(算法可能在山脊的一侧到另一侧摇摆,难以沿着最佳路径前进)
- HC may not find the optimal solution and may get stuck at a local optimum
- No information as to how much the discovered local optimum deviates from the global (or even other local optima)(算法的用户无法判断找到的解的质量有多好,或者是否接近全局最优)
- Usually no upper bound on computation time(在某些情况下,搜索可能会很快停止;而在其他情况下,尤其是在存在大量高原或山脊的解空间中,算法可能需要很长时间来寻找改进的方向)
- Success/failure of each iteration depends on starting point
- success defined as returning a local or a global optimum(从一个好的初始点开始可能直接导致全局最优解或一个好的局部最优解,而从另一个点开始可能会陷入较差的局部最优解)
5.Performance Analysis of Stochastic Local Search Methods Preliminaries (READING)
Lecture03
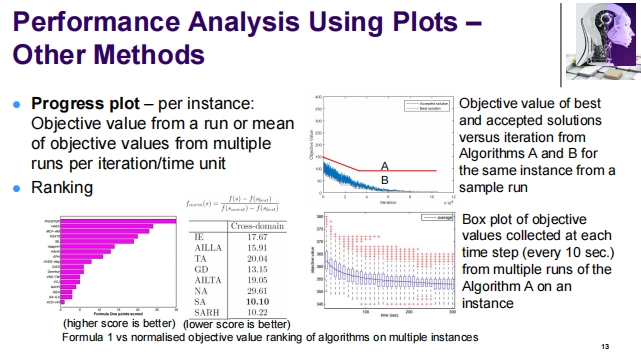
1. Performance Comparison of Stochastic Search Algorithms


2. Metaheuristics

Main Components of a Metaheuristic Search Method (r.v.)

Mechanisms for Escaping from Local Optima
- Iterate with different solutions, or restart *(*re-initialise search whenever a local optimum is encountered). (尝试不同的解决方案,或者在遇到局部最优解时重新开始)
- Initialisation could be costly
- E.g., Iterated Local Search, GRASP
- Change the search landscape
- Change the objective function (E.g., Guided Local Search)
- Use (mix) different neighbourhoods (E.g., Variable Neighbourhood Search, Hyper-heuristics)
- Use Memory (e.g., tabu search)(通过记录一定历史搜索信息来避免重复搜索)
- Accept non-improving moves: allow search using candidate solutions with equal or worse evaluation function value than the one in hand(允许使用评估函数值等于或低于当前解的候选解进行搜索)
- Could lead to long walks on plateaus (neutral regions) during the search process, potentially causing cycles – visiting of the same states
- None of the mechanisms is guaranteed to always escape effectively from local optima
Termination Criteria (Stopping Conditions) – Examples
- Stop if
- a fixed maximum number of iterations, or moves, objective function evaluations), or a fixed amount of CPU time is exceeded.(达到了预设的最大迭代次数、移动次数、目标函数评估次数,或者超过了固定的CPU时间)
- consecutive number of iterations since the last improvement in the best objective function value is larger than a specified number. (自上次目标函数最佳值改进以来,连续迭代次数超过了指定的数量)
- evidence can be given than an optimum solution has been obtained. (i.e. optimum objective value is known)(可以证明已经获得了最优解)
- no feasible solution can be obtained for a fixed number of steps/time. (a solution is feasible if it satisfies all constraints in an optimisation problem) (在固定的步数/时间内无法获得可行解)
Feasibility Example: 0/1 Knapsack Problem
How to Deal with Infeasible Solutions

- 通过设定一个固定的(死亡)惩罚值,确保不可行解的评估结果不会好于给定实例中最差的可行解。例如,可以设定一个比最差可行解还差的惩罚值,如示例中的不可行解(价值为1美元时的惩罚值设为0.5美元),无论其违反了多少约束。
- 进一步区分解的不可行级别,可以通过与违反的程度相关的惩罚来实现。例如,如果解不可行,则将其惩罚值设为最小的pi除以(2*(总重量-容量)),这样不仅惩罚了不可行解,还根据不可行的程度(即超出容量的量)区分了不同的惩罚级别,使得超重更多的解受到更大的惩罚。
3. Local Search Metaheuristics and Iterated Local Search
The Art of Searching
- Effective search techniques provide a mechanism to balance exploration and exploitation
- Exploration aims to prevent stagnation of search process getting trapped at a local optimum (避免搜索过程仅仅局限于局部最优解)
- Exploitation aims to greedily increase solution quality or probability, e.g., by exploiting the evaluation function(贪婪地提高解决方案的质量或概率)
- Aim is to design search algorithms/metaheuristics that can
- escape local optima
- balance exploration and exploitation
- make the search independent from the initial configuration(性能不应严重依赖于初始解的选择)
Iterated Local Search
- Based on visiting a sequence of locally optimal solutions by:
- perturbing the current local optimum (exploration);(扰动的目的是使算法跳出当前局部最优,以便探索解空间中的其他区域)
- applying local search/hill climbing (exploitation) after starting from the modified solution.(扰动之后深入挖掘当前区域,寻找新的局部最优解)
- A perturbation phase might consist of one or more steps
- The perturbation strength is crucial
- Too small (weak): may generate cycles(算法容易陷入循环)
- Too big (strong): good properties of the local optima are lost.(可能会完全失去当前局部最优解的有用属性)
- Acceptance criteria
- Extreme in terms of exploitation: accept only improving solutions
- Extreme in terms of exploration: accept any solution
- Other: deterministic (like threshold), probabilistic (like Simulated Annealing)
- Memory
- Very simple use: restart search if for a number of iterations no improved solution is found(在发现多次迭代没有找到改进的解决方案后,重启搜索)

ILS就是先随机翻转一个,然后再翻转基础上再去找的邻居
4. Tabu Search
Tabu Search – Overview
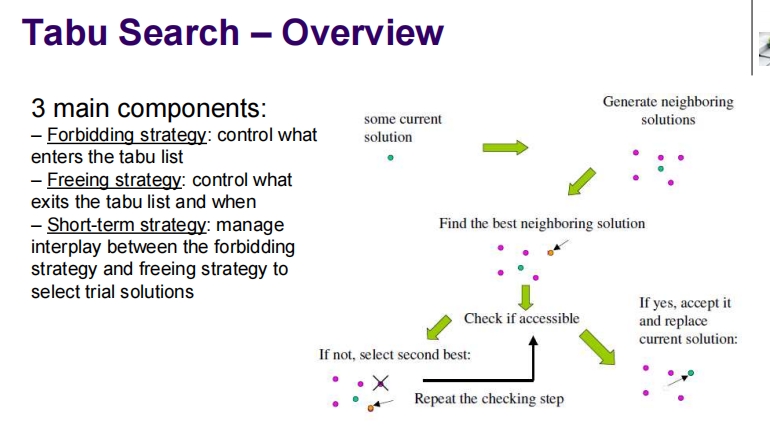

tabu会检查邻居是不是自己前n步厉遍过的
5. Introduction to Scheduling



- α 表示机器特性或环境,例如单机、并行机器等。
- β 表示处理过程或作业特性,比如作业的处理时间、截止日期、准备时间等。
- γ 表示优化准则或目标,通常是需要最小化的目标,比如最小化完成时间、最大延迟、总空闲时间等。

这张幻灯片介绍了几种典型的机器特性(α)在调度问题中的分类:
- 单机问题(Single-stage problem):这是最简单的情况,只有一台机器。
- Pm:表示有多台相同的机器并行工作。
这张幻灯片继续介绍了调度问题中的机器特性 (α) 示例:
- Pm:指有 m 台相同的机器在并行工作,每个作业 j 需要一次操作,并且可以在任何一台 m 机器上加工。
- Qm:表示 m 台机器并行工作,但是它们的速度不同。
- Rm:表示 m 台不相关的机器并行工作,对不同的作业有不同的加工速度。
在单阶段问题(Single-stage problem)中,每个作业仅在单一机器上进行一次操作。这与多阶段问题相对,后者涉及多个操作或多个机器阶段(例如流水线作业)。这种分类帮助确定解决问题的方法和算法


介绍了作业特性 (β) 的例子:
- 加工时间:作业在机器上的加工时间可能各不相同,也可能对所有作业都相同,或者甚至是单位长度。所有的加工时间都假定为整数。特定作业 j 在机器 i* 上的加工时间用 p_ij 表示。
- 交货期:作业 j 的承诺交货期或完成期限用 d_j 表示。
- 权重:作业 j 相对于系统中其他作业的重要性用 w_ j 表示。
- 发布日期:作业 j 可以开始加工的最早时间用 r_ j 表示。
- 优先级:作业之间可能存在优先关系,如果作业 k 优先于 l,则 l 的开始时间不应早于 k 的完成时间。
- 序列依赖的准备时间:作业 j 和 k 之间的设置时间用 s_jk 表示。
- 故障:表示机器不是一直可用的,可能会有故障。






Overall Summary

自我笔记

Lecture04
1. Local Search Metaheuristics and Move Acceptance Methods
Move Acceptance Methods – A Taxonomy
接受非改进的移动可以作为一种逃避局部最优的机制

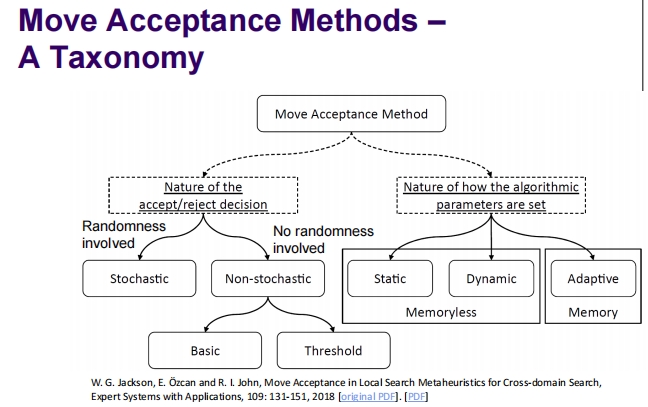

Non-stochastic Basic Move Acceptance Methods

Late Acceptance Algorithm


Non-stochastic Threshold Move Acceptance


Great Deluge – minimisation

Extended Great Deluge – minimisation

Stochastic Move Acceptance


Simulated Annealing Local Search Metaheuristic

Accepting Moves using SA

T变小,接受差解的概率变小

SA – Cooling Schedule



2. Parameter Setting Issues and Tuning Methods

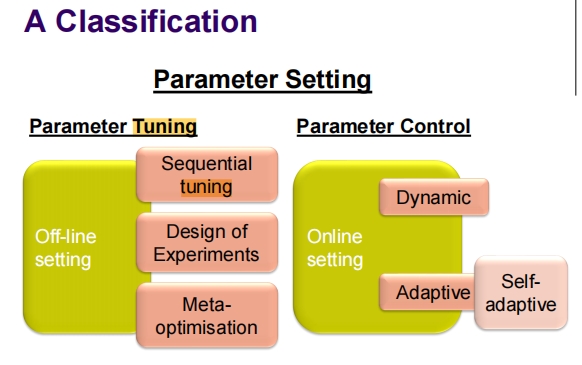

Design of Experiments – Sampling

Random Sampling

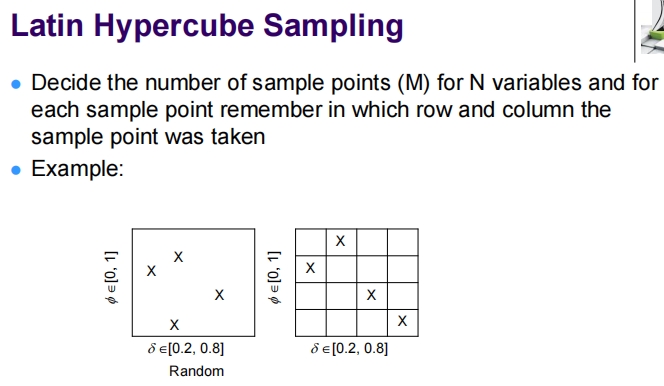
Latin Hypercube Sampling
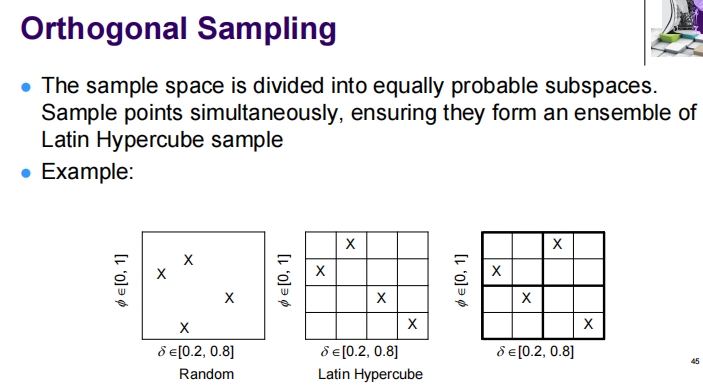
Orthogonal Sampling
Lecture05






GA Components – Reproduction

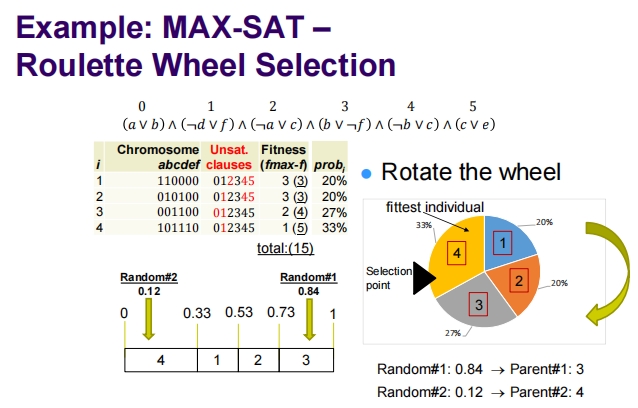
Roulette Wheel Selection

Tournament Selection


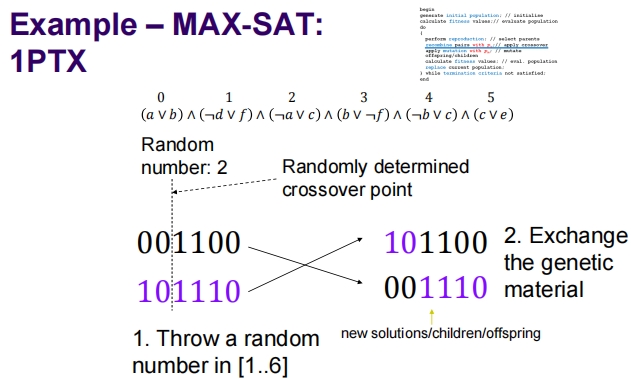
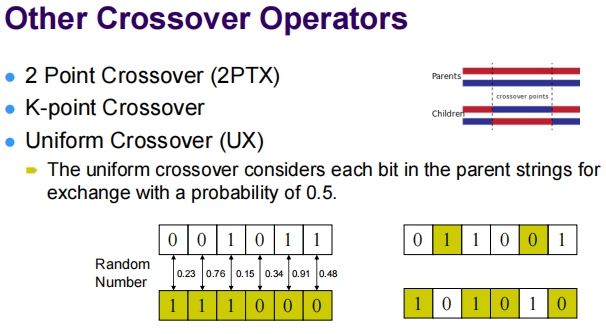
Recombination – Crossover

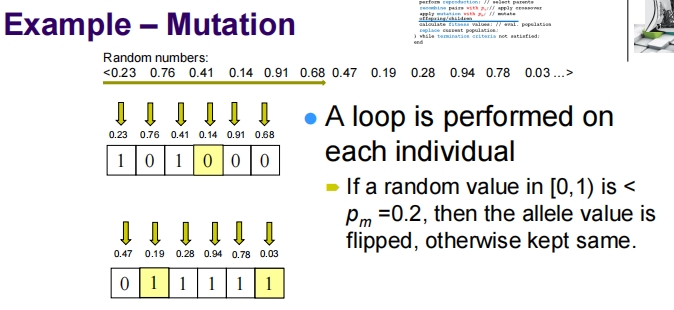
Mutation

Replacement





Memetic Algorithms
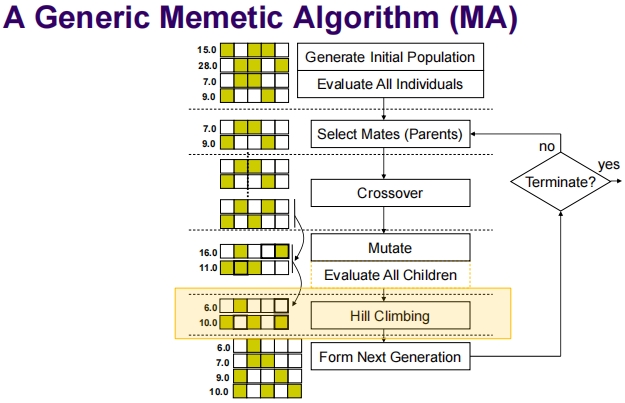


Lecture06
Benchmark Functions

Classification of benchmark (test) functions

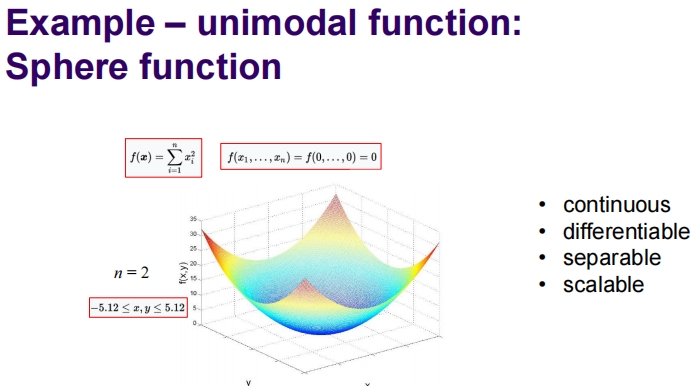
Example – unimodal function: Sphere function


Example – Sphere Function Optimisation




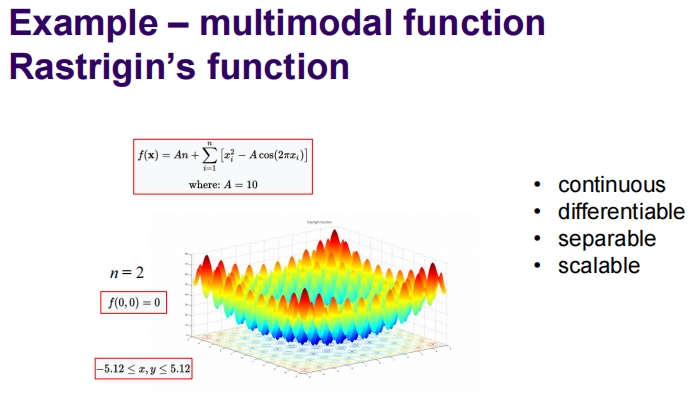
Example – multimodal function Rastrigin’s function
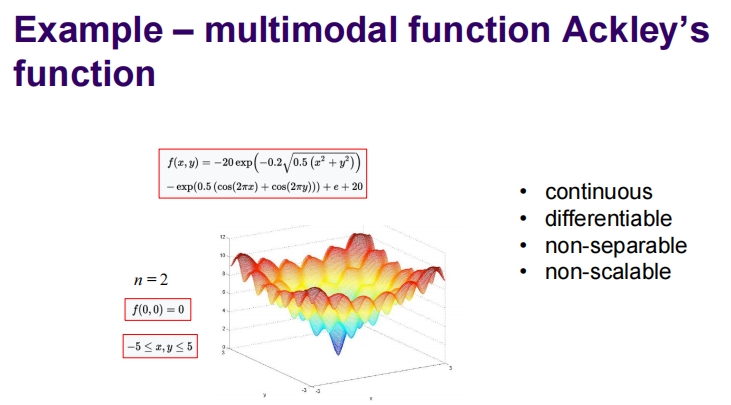
Example – multimodal function Ackley’s function
BENCHMARK FUNCTION OPTIMISATION

TRAVELLING SALESMAN PROBLEM

两个个体交换了竖线 | 后面的内容

Generic Permutation based Genetic Operators
Partially Mapped Crossover (PMX)



Order Crossover (OX)


Cycle Crossover (CX)



Multimeme Memetic Algorithms



Lecture07
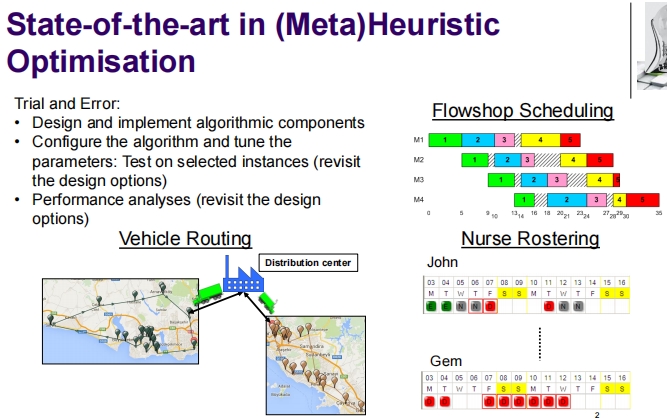
这张幻灯片介绍了在(元)启发式优化中的最新技术。主题包括:
试错法:
- 设计并实现算法组件
- 配置算法并调整参数:在选定的实例上测试(重新审视设计选项)
- 性能分析(重新审视设计选项)
**流程调度 (Flowshop Scheduling)**:
- 展示了一个流程调度问题,其中包含多个机器(M1, M2, M3, M4)和不同的任务(编号为1到5),每个任务在不同的机器上处理的时间都不相同。
**车辆路径规划 (Vehicle Routing)**:
- 展示了从一个分配中心出发的车辆路径图,说明了如何优化货物配送路线。
**护士排班 (Nurse Rostering)**:
- 为两位护士(John和Gem)展示了一周的工作班次安排,每天的班次有不同的时间和强度等级(如0-9分)。
这张幻灯片的目的是展示如何通过使用启发式和元启发式方法解决不同的优化问题,包括生产调度、物流和人员排班等。

这张幻灯片介绍了超启发式这一概念,并比较了不同的搜索空间。
超启发式
- 定义:超启发式是一种搜索方法或学习机制,用于选择或生成启发式方法以解决计算上困难的问题。
- 应用:它被描述为一种跨领域搜索的方法类。
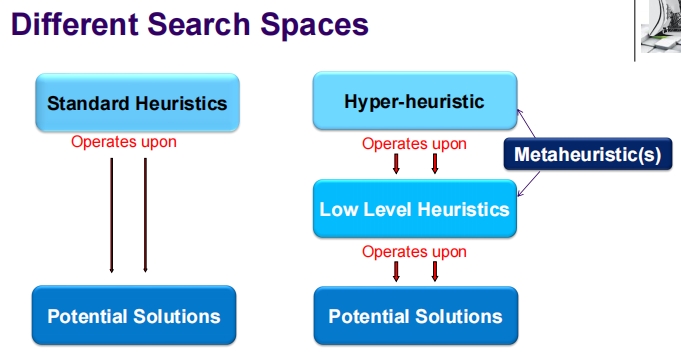
不同的搜索空间
- 标准启发式:操作在潜在解决方案上。
- 超启发式:
- 操作在低级启发式上,这些启发式又操作在潜在解决方案上。
- 可以结合元启发式来提升搜索效果。
这张幻灯片旨在解释超启发式的概念及其在解决复杂优化问题中的应用,通过比较传统启发式和超启发式在不同层级上的作用来展示其优势。

这张幻灯片主要介绍了跨领域搜索的动机、挑战和超启发式的起源。
动机 - 跨领域搜索
- 研究动机:超启发式研究的动机在于提高搜索方法的一般性和效果。研究者探索不同方法的极限,寻找更广泛适用的算法。
- 重大挑战:图表显示了从特定问题解决方案向更通用解决方案的转变,并指出尽管存在将解决方案通用化的巨大潜力,但目前还不存在一个能解决所有问题的通用求解器,这表示未来研究的重要方向。

超启发式:起源
- 时间线从1961年到2001年,标出了超启发式发展历程中的关键文献。
- 1963年:Fisher和Thompson的研究介绍了局部作业车间调度规则的概率学习组合。
- 1990-95年:这一时期出现了更多关于概率性和参数学习组合的研究。
- 1997年:进一步探索了使用多种AI方法改进ATP系统性能的可能性。
- 2001年:Cowling, Kendall和Soubeiga提出了一种超启发式方法,用于调度销售峰会,这标志着超启发式在解决实际问题中的应用。
这张幻灯片通过展示超启发式的研究历程和文献,强调了该领域从特定的问题求解向更广泛应用的发展趋势。

这张幻灯片详细介绍了超启发式用于跨领域搜索的框架以及其特点。
超启发式选择框架用于跨领域搜索
- 无需领域特定知识:使用的是一系列简单且知识贫乏的启发式方法。
- 足够健壮:能够有效处理来自各种领域的广泛问题实例。
图示解释了超启发式域与问题域之间的关系,强调超启发式主要操作在启发式上,而非直接在问题解决方案上。

超启发式的特征(初步框架)
- 操作空间:超启发式操作在启发式的搜索空间(邻域操作符)上,而不是直接在解决方案的搜索空间上。
- 目标:利用每种启发式的优势并避免其弱点。
- 无需问题特定知识:在搜索启发式(操作符)空间期间,不需要具体问题的知识。
- 易于实施和部署:实现简单,部署实用(成本低,快速)。
- 现有或计算生成的启发式:可以在超启发式中使用现有的或计算生成的启发式(操作符)。
这张幻灯片强调了超启发式的实用性和通用性,特别是在不依赖领域特定知识的情况下,如何有效地解决多领域的问题。

相关领域
- 反应式搜索(Reactive search)
- 算法选择/组合(Algorithm selection/portfolios)
- 自适应算子选择(Adaptive operator selection)
- 元学习(Meta-learning)
- 共进化/多模因算法/模因计算(Co-evolution/multimeme memetic algorithms/Memetic computing)
- 变量邻域搜索(Variable Neighbourhood Search)
- 协作(分布式)搜索(Cooperative (Distributed) Search)
- 参数控制(例如在进化算法中)(Parameter control, e.g., in EAs)
- 算法配置(Algorithm configuration)
这些领域都与超启发式有关,因为它们涉及优化搜索策略以解决复杂的问题。
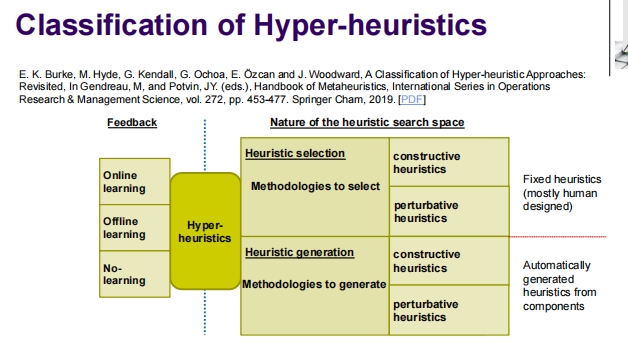
超启发式的分类
超启发式分为两大类:
- 启发式选择:基于反馈采用在线学习或离线学习,或者不涉及学习。
- 启发式生成:同样基于不同的学习策略,用于生成启发式。
进一步细分:
- 选择性方法和生成性方法均可用于构建性(constructive)启发式或扰动性(perturbative)启发式。
- 构建性启发式涉及构建解决方案的步骤,而扰动性启发式涉及修改现有解决方案的方法。
启发式的来源:
- 固定启发式:通常由人设计。
- 自动生成的启发式:从算法组件自动生成。
这张幻灯片通过展示超启发式的相关领域和详细分类,帮助理解如何使用不同的方法和策略在多种问题求解环境中应用超启发式,以提高搜索效率和效果。

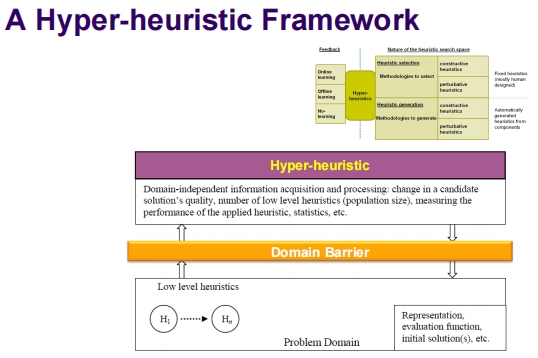
超启发式框架
- 域独立信息获取和处理:这包括候选解决方案质量的变化、低级启发式的数量(如种群大小)、应用启发式的性能、统计数据等。
- 域屏障:在超启发式和问题域之间存在一个屏障,超启发式操作在这个屏障之上,不依赖于特定问题域的信息。
- 低级启发式:从 H_1 到 H_n,表示超启发式可以操作的不同启发式方法。
- 问题域:包括问题的表示、评估函数、初始解决方案等。
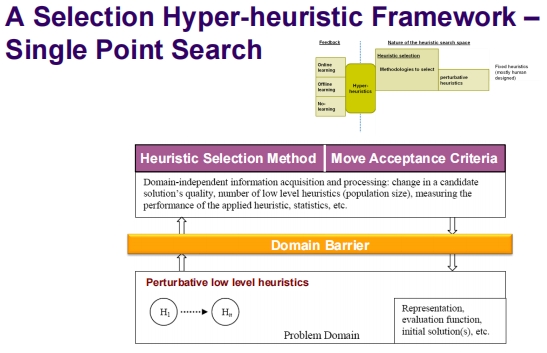
选择超启发式框架 - 单点搜索
- 启发式选择方法与移动接受标准:
- 框架使用启发式选择方法来选择最适合当前问题实例的启发式。
- 移动接受标准决定了在搜索过程中是否接受一个新的解决方案。
- 扰动性低级启发式:这些启发式修改现有的解决方案以探索新的可能解决方案。
这些框架的主要特点是它们提供了一种结构化方法来处理和应用超启发式,以便在没有特定领域知识的情况下解决各种优化
问题。这样的方法允许超启发式算法适用于多种不同的问题类型,通过选择和应用最适合当前问题环境的启发式来寻找最佳解决方案。这种方法在操作上不依赖于问题的具体细节,使其成为一个强大的工具,特别是在解决新的或未知类型的问题时。

这段代码是关于选择超启发式框架在单点搜索中的一个简单示例。它描述了超启发式搜索过程中的步骤,如下:
- 生成初始候选解决方案 p:这是搜索开始的点,所有操作都基于此初始解。
- 循环条件:循环将继续进行,直到满足终止条件(如达到最大迭代次数、找到满意的解决方案等)。
- 选择启发式 h:从启发式集合 {H₁, …, Hₙ} 中选择一个或一组启发式。这些启发式用于生成新的解决方案或改进现有的解决方案。
- 生成新的解决方案 s:通过应用选定的启发式 h 到当前候选解决方案 p 上,生成一个或多个新的解决方案。
- 决定是否接受新解决方案 s:根据某些标准(如改善的质量、成本、或其他性能指标)决定是否将新解决方案 s 作为新的候选解决方案。
- 如果接受 s:更新候选解决方案 p 为新的解决方案 s。
- 返回最终解决方案 p:当循环结束时,返回当前的候选解决方案 p,此时它是根据给定的超启发式策略找到的最优解或满意解。
这个流程利用超启发式的优势,即不依赖特定问题领域的知识,通过智能地选择和应用多种启发式来逐步优化解决方案。这种方法特别适用于解决那些难以用传统算法解决的复杂和多变的问题。
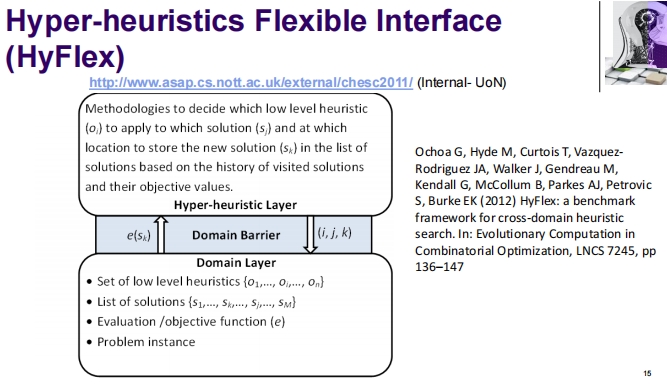
这张幻灯片详细介绍了超启发式的灵活接口系统(HyFlex)。
超启发式灵活接口(HyFlex)
HyFlex 是一个为超启发式搜索设计的框架,其特点是:
灵活性:HyFlex 提供了一个灵活的接口,定义了组件的行为并安排它们之间的交互。这允许研究者针对不同的问题域使用相同的超启发式搜索策略。
域层与超启发式层的分离:
- 域层包括:
- 一组低级启发式(O₁, …, Oₙ)
- 解决方案列表(S₁, …, Sₘ)
- 评估/目标函数(e)
- 特定问题实例
- 超启发式层则处理:
- 决定使用哪个低级启发式
- 选择解决方案和存储新解决方案的位置
- 超越“域屏障”,这意味着超启发式层在不直接涉及具体问题细节的情况下操作
- 域层包括:
方法论:提供了如何决定哪个低级启发式适用于哪个解决方案,以及新解决方案应如何根据已访问解决方案的历史和它们的目标值存储的方法。
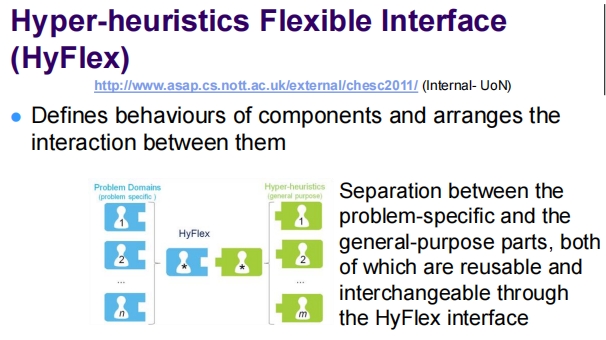
组件分离和重用:HyFlex 框架强调了问题特定部分和通用部分之间的分离,这两部分都是可重用的且可以通过 HyFlex 接口交换。
这种设计使得 HyFlex 成为跨领域搜索的有力工具,因为它允许研究者在不同的问题上重用相同的搜索策略,同时调整用于特定问题的启发式和评估方法。这不仅增加了研究的灵活性,还提高了研究效率,使得可以在更广泛的问题集上测试和优化超启发式方法。

这张幻灯片详细介绍了HyFlex v1.0 Java实现中涵盖的问题域和具体的例子,即一维离线装箱问题(1D Offline Bin Packing)。
HyFlex v1.0 Java实现
- 实现的问题域:HyFlex目前实现了六个问题域,包括MAX-SAT, Bin Packing, Flow Shop, Personnel Scheduling, TSP, 和 VRP。
- 启发式类型:包括突变型(mutational),重新创建(ruin-recreate),局部搜索(local search),和交叉(crossover)。
- 搜索参数:强度和搜索深度。
在给定的表格中,列出了各个问题域可用的启发式(标记为MU0, HC0等),这些启发式通过HyFlex框架进行调用和管理。

一维离线装箱问题
- 问题描述:需要将一系列大小为 ( s_i ) 的物品打包到容量为 ( C ) 的箱子中,目标是最小化使用的箱子数量。
- 约束条件:
- 物品大小 ( s_i ) 是整数,并且 ( 1 \leq s_i \leq C )。
- 每个箱子的容量是固定的。
- 确保没有一个箱子的容量被超过。

例子
给定物品集合:共有7个物品,大小分别为 ( S = [8, 1, 7, 6, 2, 2, 4] )。
箱子大小:( C = 10 )。
目标:尽可能少地使用箱子。
示例解决方案:在示例中,物品被分配到三个箱子中。
- 箱子1:物品大小为8,2。
- 箱子2:物品大小为1,2,7。
- 箱子3:物品大小为6, 4。
这个问题是一个标准的NP难问题,代表了计算中的一类重要优化问题,HyFlex工具在处理此类问题时,通过不同的启发式策略来寻求最优或近似最优解。

这张幻灯片提供了关于“Bin Packing”问题域中使用的几种低级启发式算法的具体信息,这些启发式包括突变启发式和局部搜索启发式。
低级突变启发式
这些启发式主要关注通过简单修改来探索解决方案空间:
- 突变强度:参数“intensity of mutation”控制突变的频率,范围从0.2(重复1次)到1.0(重复5次)。
- 交换(Swap, MU₀):随机选择两个不同的物品,并在有空间的情况下交换它们。
- 分割箱子(Split a Bin, MU₁):随机选择一个箱子,如果其包含的物品数量多于平均数,则将该箱子分割为两个,每个新箱子包含原箱子一半的物品。
- 重新打包最低填充箱子(Repack the Lowest Filled Bin, MU₂):移除最少填充箱子中的所有物品,并尝试使用最佳适应启发式将它们重新分配到其他箱子中。
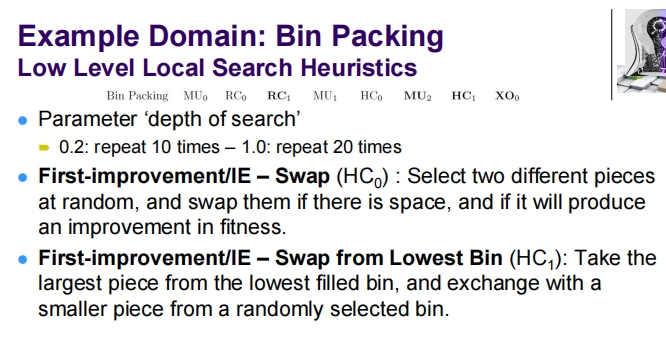
低级局部搜索启发式
这些启发式专注于通过局部改变来改善已有解:
- 搜索深度:参数“depth of search”控制重复搜索的次数,范围从0.2(重复10次)到1.0(重复20次)。
- 首次改进/交换(First-improvement/IE – Swap, HC₀):随机选择两个不同的物品进行交换,前提是这样做可以改善总体适应度。
- 首次改进/从最低填充箱子中交换(First-improvement/IE – Swap from Lowest Bin, HC₁):从填充最少的箱子中取出最大的物品,并尝试与从随机选定的箱子中选出的较小物品交换。
这些启发式通过不同的策略寻求解决方案的局部改进或全新构建,从而在保证不超过箱子容量的同时,尽可能减少使用的箱子数。通过这种方式,HyFlex 框架允许对“Bin Packing”这一NP难问题进行高效的搜索和优化处理。

这张幻灯片介绍了在一维装箱问题领域中使用的一些更具破坏性的启发式策略,即“破坏与重建”启发式,以及一个高级的交叉方法。
破坏与重建启发式
这类启发式的核心思想是通过破坏现有解的一部分来创造新的可能空间,然后重新构建以尝试找到更优的解。
突变强度参数(intensity of mutation):这个参数控制破坏的程度。
- 0.2: 破坏3个箱子
- 0.4: 破坏6个箱子
- 0.6: 破坏9个箱子
- 0.8: 破坏12个箱子
- 1.0: 破坏15个箱子
破坏最高填充的箱子(Destroy x Highest Bins, RC₀):选择填充最多的x个箱子,将里面的所有物品移出。
破坏最低填充的箱子(Destroy x Lowest Bins, RC₁):选择填充最少的x个箱子,将里面的所有物品移出。
高级交叉方法
- 外显子洗牌交叉(Exon Shuffling Crossover, XO₀):
- 这种交叉方法通过模拟生物学中的外显子重组机制来改进解决方案。在遗传算法中,它可以帮助发现通过单一父代未能探索到的新解决方案空间。
- 引用文献:Philip Rohlfshagen 和 John Bullinaria 在 2007 年的论文提出了这种交叉方法,专门用于解决困难的装箱问题。
通过这种类型的启发式,系统能够大幅度调整解决方案结构,可能发现比当前解更有效的新解。这些方法特别适用于寻找问题解决的全局最优解,尤其是在解空间复杂或者解决方案质量差异大的情况下。
这张幻灯片详细说明了在超启发式框架中使用的两种启发式选择策略:贪心选择(Greedy Selection)和基于强化学习的选择(Reinforcement Learning Selection)。
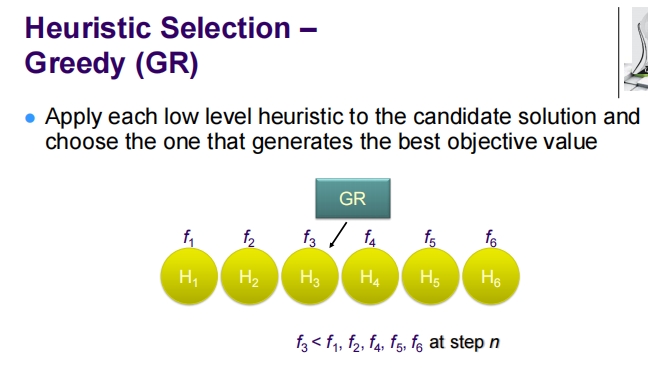
贪心选择 (Greedy, GR)
- 操作方式:应用每一个低级启发式到候选解决方案,然后选择产生最佳目标值的启发式。
- 过程示意:
- 在每一步 (n),将 (H_1) 到 (H_6) 这六个启发式分别应用于当前解决方案。
- 每个启发式 (H_i) 生成一个目标函数值 (f_i)。
- 选择在该步骤产生最佳目标函数值 (f_3 < f_1, f_2, f_4, f_5, f_6) 的启发式 (H_3)。

强化学习选择 (Reinforcement Learning, RL)
- 基本概念:
- 这是一种机器学习技术,灵感来源于心理学中的奖励与惩罚理论。
- 关注如何在环境中采取行动以最大化长期奖励。
- 操作原理:
- 为每个启发式维护一个得分。
- 如果某个启发式应用后改善了解决方案(即移动是积极的),则增加其得分(例如 +1)。
- 如果启发式应用后未改善解决方案,则减少其得分(例如 -1)。
这两种方法都是解决优化问题时常用的策略,贪心选择侧重于即时的最优解,而强化学习选择则侧重于通过不断的试错过程学习如何取得长期的最优解。在实际应用中,选择哪种方法取决于问题的具体需求和复杂性。贪心方法简单直接,适合问题相对单一且解空间不复杂的情况。而强化学习方法则适合于解空间复杂、需要适应性更强策略的问题环境。

这张幻灯片详细介绍了强化学习(RL)在启发式选择中的应用,并引入了选择函数(Choice Function, CF)作为一种更复杂的决策机制。
强化学习(RL)示例迭代
- 上下文:在特定领域实现中有两个低级启发式 ( h_1 ) 和 ( h_2 )。
- 操作步骤:
- 选择启发式:选择得分最高的启发式,例如 ( h_2 ) 有最高得分 5。
- 应用启发式:将 ( h_2 ) 应用到当前解决方案 ( s ) 上,生成新解 ( s’ )。
- 更新分数:
- 如果 ( s’ ) 是一个改善或等同的解决方案,增加 ( h_2 ) 的得分。
- 如果 ( s’ ) 恶化了解决方案,减少 ( h_2 ) 的得分。例如,从 5 减到 4。

启发式选择 - 选择函数(CF)
功能:选择函数维护每个启发式的性能记录,包括三个标准:
- 单独性能:启发式单独时的表现。
- 与其他启发式共同表现:在与其他启发式组合时的表现。
- 自上次调用以来的时间:距离最后一次被调用的时间。
计算方法:
- ( f_1(h_j) ) 代表单独性能,与每次使用后的表现变化有关。
- ( f_2(h_k, h_j) ) 表示在组合使用时的表现。
- ( f_3(h_j) ) 衡量自上次调用以来的时间。
选择函数公式:
[
F_n(h_j) = \alpha_n f_1(h_j) + \beta_n f_2(h_k, h_j) + \gamma_n f_3(h_j)
]
其中,( \alpha_n ),( \beta_n ),和 ( \gamma_n ) 是调节这三个因素重要性的权重参数。
这种启发式选择方法利用复合评价标准,不仅考虑每个启发式的直接表现,还考虑其与其他启发式的相互作用和时间因素,使得启发式选择更加精确和适应性强。这种方法特别适用于需要动态调整启发式策略的复杂优化问题,能够有效提升搜索过程的效率和解决方案的质量。
这张幻灯片详细说明了启发式选择的选择函数(Choice Function, CF)机制,并通过一个简化的示例迭代来阐释其操作方式。
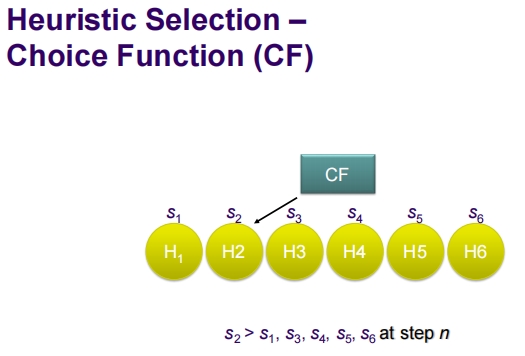
选择函数 (CF)
- 目的:选择函数用于根据多个标准评估并选择最佳启发式。
- 操作流程:
- 启发式 ( H_1, H_2, …, H_6 ) 产生相应的解 ( S_1, S_2, …, S_6 )。
- 在给定步骤 ( n ) 中,比较各解的性能,并选择性能最佳的启发式进行下一步操作。

简化的选择函数 - 示例迭代
环境设置:
- 有两个低级启发式 ( h_1 ) 和 ( h_2 )。
- 每个启发式有两个得分:( f_1 ) 和 ( f_2 ),分别表示性能分。
- 权重 ( \alpha, \beta, \gamma ) 固定,简化计算。
迭代过程:
- 步骤 i:( h_2 ) 在先前步骤被调用,得分如下:
- ( h_1: f_1 = 3, f_2 = 5 )
- ( h_2: f_1 = 5, f_2 = 3 )
- 选择函数 ( CF ) 用于计算得分:( F(h_1) = \alpha f_1(h_1) + \beta f_2(h_1, h_2) ) 和 ( F(h_2) = \alpha f_1(h_2) + \beta f_2(h_2, h_1) )。
- 选择和应用:根据 ( CF ) 得分选择 ( h_2 ) 并应用到当前解决方案。
- 更新得分:如果 ( h_2 ) 提高了解决方案,则增加其得分;如果未改善,则减少。
- 步骤 i:( h_2 ) 在先前步骤被调用,得分如下:
步骤 i+1 更新后:
- ( h_1 ) 和 ( h_2 ) 的新分数分别调整,反映它们在最新迭代中的表现。
- 如果 ( h_2 ) 改善了解决方案,( f_1 ) 和 ( f_2 ) 会相应增加。
这个例子展示了如何利用固定的权重参数和性能得分来动态选择最优启发式。选择函数通过综合考虑单个启发式的历史表现和与其他启发式的协同作用,实现对启发式的智能选择,这对于处理复杂的优化问题至关重要。
这张幻灯片呈现了超启发式中的“移动接受”策略以及一些关于超启发式的常见误解。
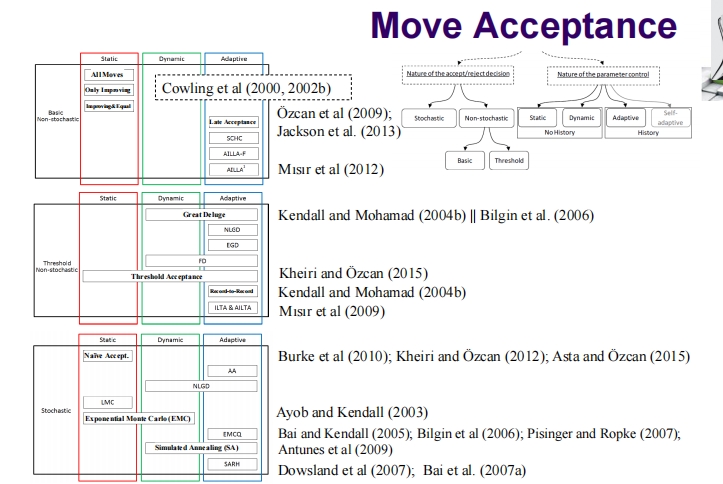
移动接受策略
- 分类:移动接受策略分为多种类型,包括:
- 静态接受:总是接受或总是拒绝特定类型的移动。
- 动态接受:根据一定规则改变接受策略,例如基于搜索进展。
- 自适应接受:根据算法性能的历史数据自动调整接受标准。
- 其他方法:如模拟退火(Simulated Annealing, SA)、LATE Acceptance等。

关于超启发式的几个误解 - 个人观点
- 参数调整:超启发式不需要参数调整。这是一个误解,因为虽然超启发式旨在减少对参数调整的需求,但实际上在实现最优性能时仍可能需要调整。
- 测试公平性:所有超启发式都在公平的设置下测试(例如使用 HyFlex)。这包括为调整时间和实例分配相同的资源。
- 应用简便性:将超启发式应用到新领域很容易。这可能不总是正确的,因为每个新领域都可能需要对启发式方法进行特定调整以达到最佳效果。
- 领域特定信息:领域特定信息不应传递给超启发式。目标值不是领域特定信息,所有启发式都可以使用它。
这些点提供了对超启发式理解和应用的深入洞察,指出了人们对其功能和性能可能存在的一些常见误区。通过阐明这些误解,可以更有效地利用超启发式解决各种优化问题。

这张幻灯片总结了最近在选择性超启发式领域的研究重点:
1. 现有超启发式的优化与调整
- 性能优化:对现有的超启发式或元启发式进行调整和配置,以提升其在跨领域搜索中的性能。
2. 超启发式的新领域应用
- 新问题领域:将已有的超启发式方法应用到新的问题领域,测试其适用性和效果。
3. 新超启发式的创造与测试
- 新兴超启发式:基于元启发式和数据科学技术开发的新型超启发式正在出现,这些包括:
- 多阶段方法:迭代多个阶段的方法,每个阶段针对特定子问题或优化目标。
- 生成超启发式:通过自动生成的过程创建新的启发式方法。
- 多目标超启发式:同时考虑多个优化目标,为复杂决策问题提供解决方案。
4. 混合方法的出现
- 混合方法:结合精确和近似方法,或者构造性和扰动性方法,来应对更复杂的优化问题,这些方法通常能更全面地探索解空间,提高解的质量和搜索效率。
这些研究焦点显示了超启发式领域的动态发展,随着问题的复杂性增加和计算技术的进步,新方法不断涌现,现有方法也在不断优化中。这种进展表明,超启发式正在成为解决各种优化问题的强大工具。
An Iterated Multi-stage Selection Hyper-heuristic
这张幻灯片描述了超启发式框架的一般架构,以及第一阶段超启发式的具体实现细节。
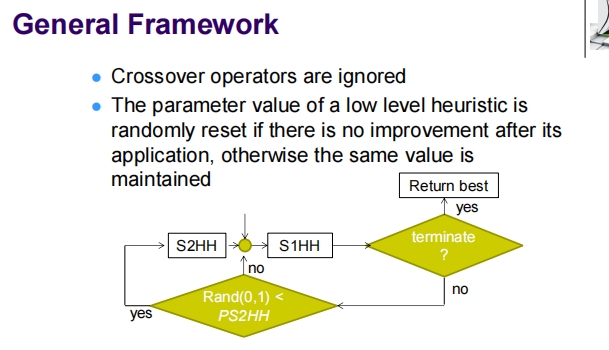
通用框架
- 交叉算子被忽略:在该框架中,不考虑交叉算子的应用。
- 参数的随机重置:如果低级启发式在应用后没有改善,其参数值将被随机重置;如果有改善,保持当前参数值。
- 流程图解释:
- 如果随机数
Rand(0,1)小于某个概率阈值PS2HH,则继续使用第二阶段超启发式S2HH,否则切换到第一阶段超启发式S1HH。 - 如果达到终止条件,返回最佳解决方案并终止。
- 如果随机数

第一阶段超启发式
- 启发式选择:选择低级启发式
i的概率基于其得分,计算公式为score_i / Σ_k(score_k),其中score_k是所有启发式的得分总和。 - 启发式应用:应用选定的启发式到当前问题。
- 接受/拒绝决策:基于一个自适应的阈值接受方法,决定是否接受由启发式产生的新解。
- 阶段结束条件:如果超过了设定的时长
s_1而没有任何改进,第一阶段终止。
这个框架和实现细节突出了超启发式方法在保持简单的同时如何有效地探索和利用搜索空间。通过动态调整和随机性的引入,它旨在适应多样的问题环境,并在没有明显进展的情况下避免过度投资于任何单一启发式。此外,通过切换不同阶段的超启发式,能够根据问题解决过程中的动态变化调整搜索策略,从而提高整体搜索效率和效果。

这张幻灯片介绍了一种自适应阈值移动接受方法,旨在动态调整超启发式中的解决方案接受标准,并提供了一个行为图示以展示这种方法的实际应用效果。
自适应阈值移动接受方法
接受标准:
- 移动会被接受如果
S_new(新解)比S_current(当前解)好,或者如果S_new比(1 + ε)f(S_beststage)好,其中S_beststage是某个阶段的最优解。 ε是一个基于当前最佳解的性能变化的动态调整值,计算方式为log(f(S_beststage) / f(S_current)) + c_i,其中c_i是预设的整数值列表C的元素。
- 移动会被接受如果
阈值更新:
ε的值在无改进持续一段时间d后会更新。c_i值在阶段2之前或期间更新,在阶段1固定。
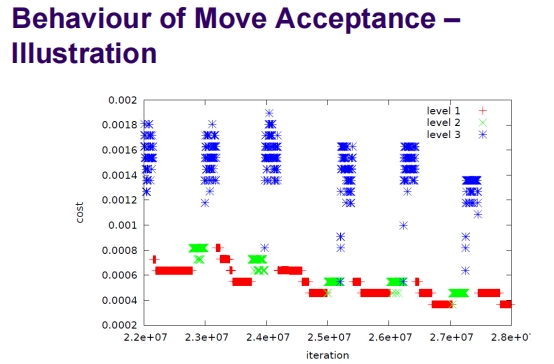
行为图示说明
- 图示:
- 展示了随着迭代进行,接受标准
ε如何变化,其中不同颜色和符号代表不同的评级层级。 - 每一层级对应一个特定的
c_i值,显示随着迭代次数增加,如何调整阈值以应对算法进展。
- 展示了随着迭代进行,接受标准
这种自适应阈值方法允许算法在搜索过程中更灵活地接受或拒绝新解,以此提高搜索效率和解决方案的质量。通过动态调整阈值,该方法可以更好地平衡探索和利用,适应于多变的搜索环境,尤其是在解决复杂或变化快速的优化问题时。此方法的应用有助于避免过早收敛于局部最优解,从而增加找到全局最优解的可能性。
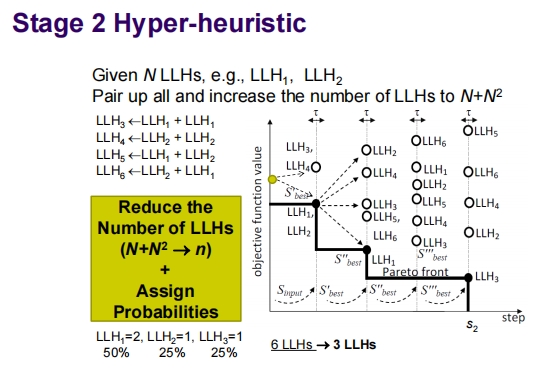
这张幻灯片介绍了一个两阶段的超启发式框架,并且展示了该框架中的参数调整策略。
第二阶段超启发式 (Stage 2 Hyper-heuristic)
概述:这个阶段的目标是通过配对和重新组合现有的低级启发式 (LLHs) 来增加启发式的数量,从 N 个LLHs增加到 N+N^2 个。然后,通过一定的减少策略,将这些启发式数量减少到一个更管理的数量,例如从 6 个LLHs减少到 3 个。
配对和增加:
- 例如,从两个基础启发式 LLH1 和 LLH2 出发,通过组合形成更多的启发式,如 LLH3 = LLH1 + LLH1, LLH4 = LLH1 + LLH2。
减少数量:
- 使用一种基于概率的方法来减少启发式的数量,确保最有用的启发式被保留。
- 例如,基于它们的性能分配概率,如 LLH1 的概率是 50%,而 LLH2 和 LLH3 的概率各为 25%。

参数调整
- 参数:提出了六个系统参数,需要根据实际应用进行调整:
τ:时间间隔(以毫秒为单位),例如 {10, 15, 20}。d:无改进的持续时间(以秒为单位),例如 {7, 9, 10, 12}。s1和s2:分别为两个阶段的持续时间(以秒为单位)和步骤数(迭代数),例如s1= {10, 15, 20, 25},s2= {3, 5, 10, 15}。PS2HH:第二阶段启发式的概率设置,例如 {0.1, 0.3, 0.6, 0.9, 1.0}。C:用于调整ε值的循环列表,例如 。
这些参数和设置允许超启发式框架在多样化的问题环境中灵活应用,通过动态调整参数以达到更优的搜索性能。参数调整的策略确保了超启发式可以在保持高效搜索的同时,适应不同的问题和搜索条件。
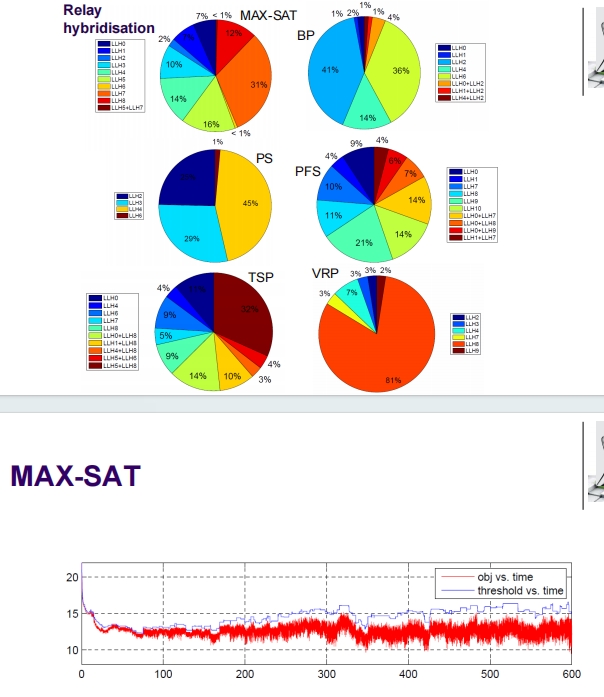
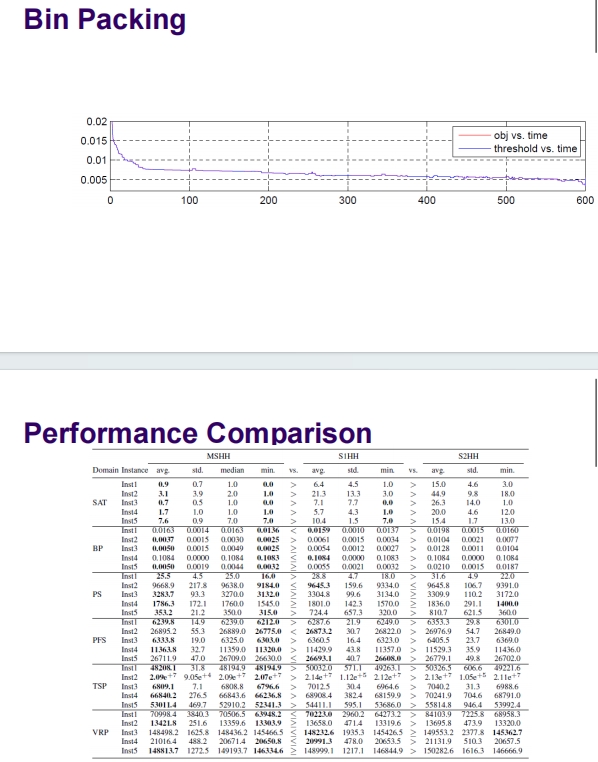

两种超启发式的有效结合:
- 提出的使用两种超启发式的方法有效地协同作用,产生了一个易于实施、易于维护并且在跨领域搜索中成功的超启发式系统。这说明整合的方法允许在各种领域中更灵活和稳健地解决问题。
自适应阈值移动接受机制:
- 自适应阈值移动接受机制捕捉到了启发式可以产生的改进程度与实现这些改进所需步骤数量之间的权衡。该机制基于算法的性能动态调整其行为,帮助算法有效地平衡深入探索搜索空间和利用已知好的解决方案之间的关系。
这些结论表明,超启发式方法的应用前景广泛,能够在解决复杂的多域问题中通过动态调整性能表现出高效的适应性。
Parameter Tuning for Cross domain Heuristic Search

跨领域参数调整研究
- 研究背景:先前的研究表明,在HyFlex的六个问题领域中,稳态遗传算法(SSMA)表现优于其跨代版本。
- 本研究:
- 性能调查:研究扩展到了九个问题领域,每个领域包含五个实例,以进一步验证SSMA的性能。
- 参数调整:使用田口方法(Taguchi design of experiments,一种正交数组测试方法)进行参数调整,以优化算法性能。

稳态遗传算法
算法步骤:
- 初始化:创建一个固定大小的种群。
- 参数设置:为突变强度(IoM)、搜索深度(DoS)和锦标赛规模(toursize)设定参数值。
- 循环过程:
- 选择两个父代。
- 应用交叉和突变操作生成子代。
- 通过局部搜索方法优化子代。
- 将种群中最差的个体替换为新生成的子代。
- 重复上述过程直至满足终止条件。
关键操作:
- 选择:通过锦标赛选择法选出父代。
- 交叉和突变:对选择的父代进行交叉和突变操作,生成子代。
- 局部搜索:对子代应用局部搜索(如爬山法)进行优化。
- 替换:将种群中的最差个体替换为优化后的子代。
这种算法结合了遗传算法的全局搜索能力和局部搜索算法的精细调优能力,通过动态调整参数和持续的优化过程,旨在解决复杂的优化问题,并在多个领域中寻找有效的解决方案。通过参数调整研究,进一步提高了算法在不同领域的适应性和效率。
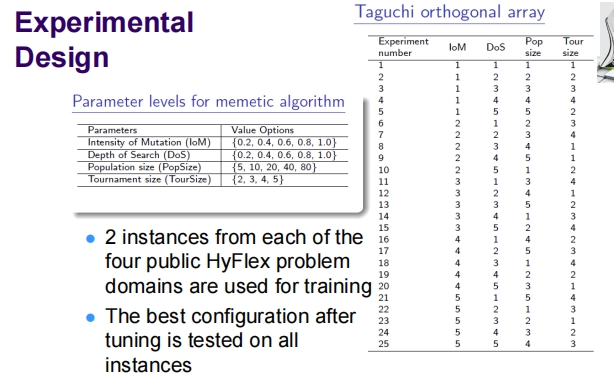
这张幻灯片详细介绍了一个关于遗传算法的实验设计,采用田口方法进行参数优化,并测试了不同的参数设置以找到最佳配置。
实验设计
参数水平:为遗传算法设置了几个关键参数的不同水平:
- 突变强度(Intensity of Mutation, IoM):从0.2到1.0不等,共六个级别。
- 搜索深度(Depth of Search, DoS):从0.2到1.0不等,共六个级别。
- 种群大小(Population size, PopSize):从5到80不等,共五个级别。
- 锦标赛大小(Tournament size, TourSize):从2到5不等,共四个级别。
田口正交阵列:实验通过田口正交阵列设计,列出了25组实验,每组实验中所有参数都有特定的配置水平。这种设计方法允许系统地探索和评估参数组合对算法性能的影响,同时减少所需的实验次数。
实验流程
- 训练实例:选取了HyFlex的四个公开问题域中的两个实例用于训练。
- 参数调优:通过在训练实例上测试不同的参数组合,找到表现最佳的配置。
- 全面测试:将调优后的最佳配置应用于所有实例,以验证其效果和适用性。
目的和意义
- 优化性能:通过田口方法的系统化参数调整,寻求在多个问题域中都表现良好的遗传算法配置。
- 减少实验负担:正交阵列设计减少了必要的实验数量,同时保证了广泛的参数覆盖,提高了实验的效率和结果的可靠性。
这种方法的使用为遗传算法和其他可能的启发式或超启发式算法提供了一个有效的参数调优和性能评估框架,是解决复杂优化问题时一个非常实用的工具。
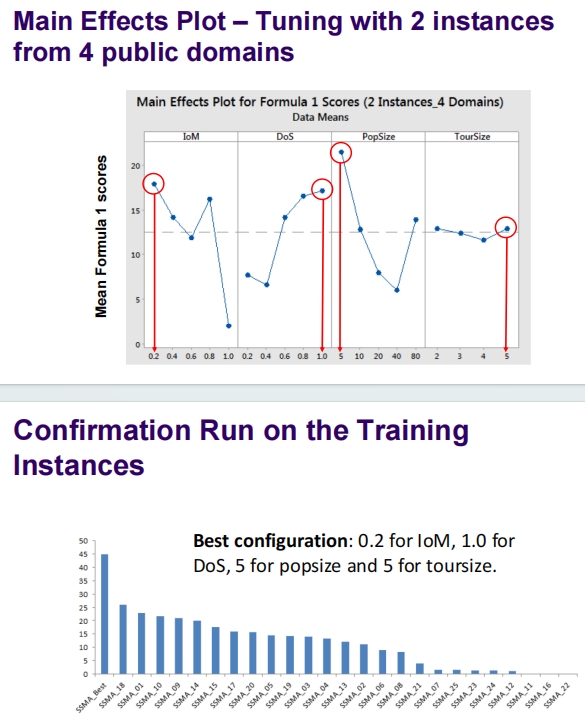
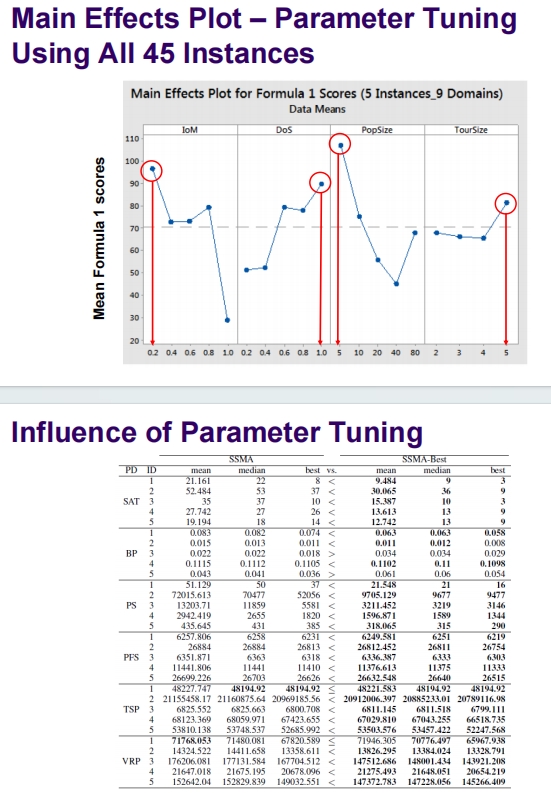

这段文字描述了在特定设置下(锦标赛大小和种群大小都为5),稳态自适应遗传算法(SSMA)的行为及其对算法性能的影响:
稳态自适应遗传算法(SSMA)的设置影响
- 选择策略:在这个特定的设置下,SSMA选择性能最好的个体作为两个父代,进行交叉操作。
- 交叉操作后的结果:由于两个父代相同,所得到的新后代将与父代完全相同,这意味着交叉操作没有产生新的遗传变异。
- 交叉操作的影响:对于HyFlex的问题领域和实例,交叉操作似乎并没有对SSMA的总体性能产生积极的影响。这表明在这些问题领域中,通过交叉产生新的解决方案的策略可能不如其他方法有效。
SSMA的表现
- 算法表现:在最佳设置下,SSMA实际上表现得更像是基于单点搜索的算法,而不是多点搜索,这使得整体算法更类似于迭代局部搜索。在这种搜索中,突变后通常会跟随一个局部搜索步骤,以优化每一步产生的解决方案。
结论
- 这种发现表明,对于某些问题领域,优化算法设置和选择合适的遗传操作对于提高算法效率至关重要。SSMA在特定条件下可能需要重新考虑交叉操作的实用性,以便更有效地利用计算资源进行问题求解。
- 在实际应用中,可能需要根据问题的特性和复杂度调整算法的参数和操作策略,以确保最优或接近最优的解决方案。
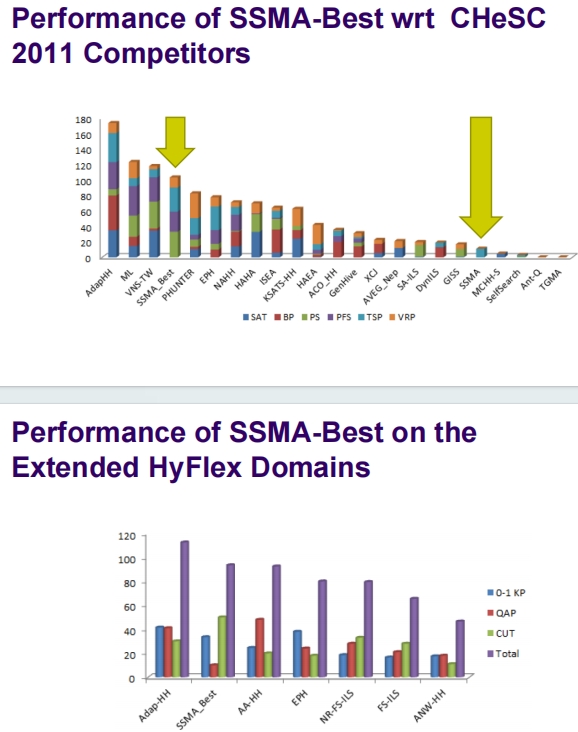

这张幻灯片总结了关于稳态自适应遗传算法(SSMA-Best)的研究结论,特别强调了参数调整在跨领域搜索中的重要性和实际效用。
结论概述
参数调整的实际价值:
- 研究强调参数调整在跨领域搜索中具有真实的价值。通过精确的参数调整,可以显著提升算法在不同问题领域中的性能。
SSMA-Best的成功表现:
- 调整实验显示,SSMA-Best在性能上显著超过了其他两种遗传算法变体,甚至一些在CHeSC2011竞赛中的其他搜索方法。这表明SSMA-Best具有优越的搜索能力和适应性。
实证结果的关键观察:
- 实证结果表明,在这种情况下应避免使用交叉操作,因为它可能不会产生有益的新解。相反,单点基于搜索的方法更为推荐,因为它更能有效地探索问题空间,避免复杂的交叉操作可能带来的效率低下问题。
实际应用意义
- 这些结论对于优化算法的设计和应用提供了重要的指导,尤其是在需要处理多种不同类型问题的情况下。选择正确的参数和适当的遗传操作对于实现高效和有效的搜索至关重要。
- 研究还暗示,在进行跨领域搜索时,应根据具体问题的特性和需求来调整算法策略,而不是一味追求通用解决方案。这种方法能够更好地利用计算资源,提高问题解决的成功率和效率。
总的来说,这项研究提供了对遗传算法在多领域应用中的深入见解,并指出了改进算法性能的具体途径。
Lecture08
Configuring/Tuning of Hyper/Metaheuristics for Cross domain Search

这幅图显示的是一篇关于如何配置或调整超启发式或元启发式算法以用于跨领域搜索的科学论文的封面和部分内容。文中提到了一个重新配置的修改版选择函数超启发式算法,这种算法控制了一元和二元运算符。图中展示了一些图表,这些图表可能是关于算法性能的比较。
文档还包括了一些公式,这些公式展示了算法的数学描述,以及在不同设置(如是否包括交叉算子)下,这些函数是如何变化的。
总体而言,这是一份涉及高级算法研究和应用的科学研究文件,目的在于通过调整和配置特定的算法功能来优化跨领域的搜索效率和效果。
A Graph-based Hyper-heuristic
这张图是关于图着色问题的讲解材料。图着色问题是图论中一个常见的问题,涉及到如何给图的顶点着色,以满足特定的约束条件。
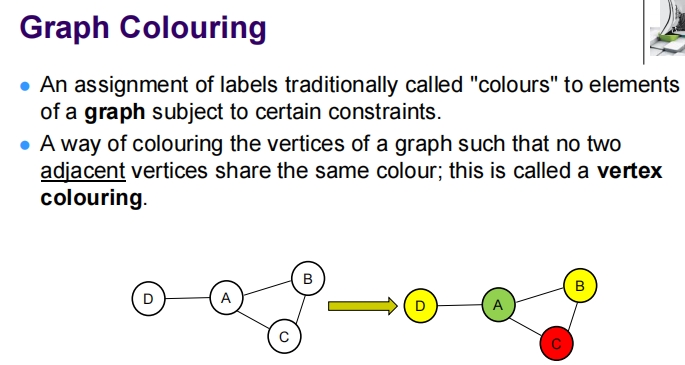
第一部分讲述了基本的图着色概念,即给图的顶点分配标签(通常称为“颜色”),使得任何两个相邻的顶点都不共享相同的颜色。这种顶点的着色方式称为顶点着色。图中展示了一个简单的例子,其中四个顶点A、B、C、D通过边连接,展示了在没有颜色冲突的情况下如何对这些顶点进行着色。
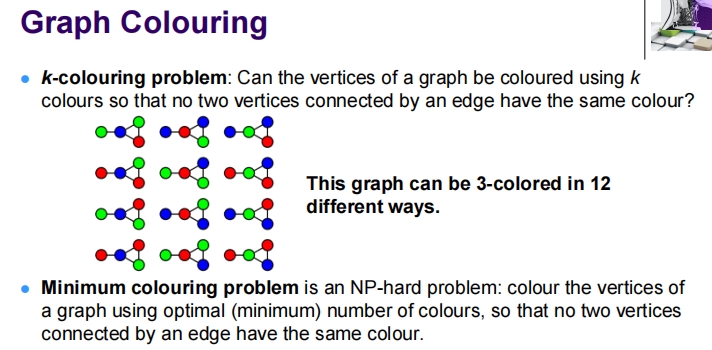
第二部分深入讨论了“k-着色问题”,即询问是否可以使用k种颜色来着色图的顶点,使得连接的顶点不会有相同的颜色。另外,还提到了最小着色问题,这是一个NP-难题,即用最少的颜色给图的顶点着色,使得相连的顶点没有相同的颜色。图中给出了一个例子,显示一个图可以用3种颜色以12种不同的方式进行着色。
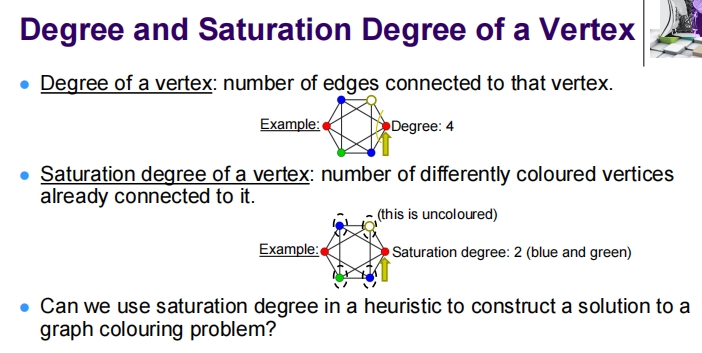
这幅图展示了关于图论中顶点的度和饱和度概念,以及如何应用这些概念来解决图着色问题的讲解材料。
顶点的度和饱和度:
- 度(Degree):一个顶点的度是与该顶点相连的边的数量。例如,图中有一个顶点的度为4。
- 饱和度(Saturation Degree):一个顶点的饱和度是与该顶点相连的、已经着色的不同颜色的顶点数量。例如,图中一个未着色的顶点与两个不同颜色(蓝色和绿色)的顶点相连,所以其饱和度为2。
提出了一个问题:我们能否使用顶点的饱和度作为启发式方法来构建图着色问题的解决方案?

图着色启发式方法:
- 最大度法则(Largest Degree):
- 计算所有顶点的度。
- 按度从大到小对顶点排序。
- 从列表中选取度最大的顶点,用一个与其相邻顶点不同的颜色进行着色。
- 从列表中删除已着色的顶点,重复以上步骤,直到所有顶点都着色。
图中展示了一个例子,说明了如何按照顶点的度对它们进行排序和着色,从而解决图着色问题。这种方法试图通过优先考虑连接较多的顶点来简化问题,理论上这些顶点着色的限制条件最为复杂,因此先着色有助于减少整体的冲突可能。
这些概念和方法在解决涉及网络、调度、分配问题等领域的图着色问题中非常有用,尤其是在计算机科学和数学中。
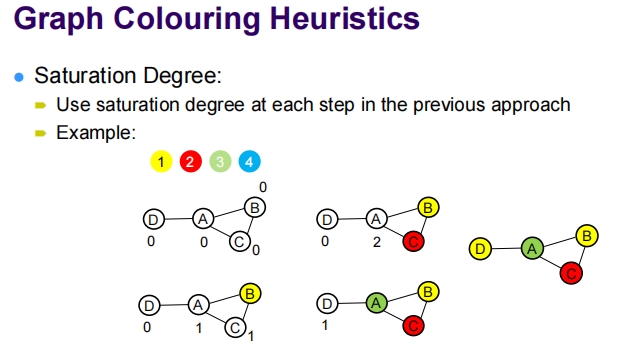
这张图解释了如何在图着色问题中使用顶点的饱和度作为一种启发式方法。饱和度启发式是一种用于选择着色顺序的技术,优先考虑那些如果未着色将有更多限制的顶点。
饱和度启发式的步骤如下:
- 计算饱和度:每个顶点的饱和度是指与该顶点相连的、已经着色的不同颜色的顶点数量。
- 选择顶点着色:在每一步中,选择饱和度最高的顶点进行着色。如果饱和度相同,则可以选择任一顶点。
- 选择颜色:为选定的顶点选择最小的可用颜色,即不与相邻顶点的颜色冲突的最小编号颜色。

这些幻灯片涉及考试时间表的排定,包括考试的排定约束、本地搜索启发式和模拟退火算法的设计。
考试时间表排定
主要内容:
- 任务:需要为一系列的考试(( e_1, e_2, …, e_E ))安排时间和教室,考试被不同的学生(( s_1, s_2, …, s_S ))参加。
- 时间段和教室:考试必须在限定的时间段(( t_1, t_2, …, t_T ))和特定的教室(( r_1, r_2, …, r_R ))内进行。
约束条件分为两类:
- 硬约束:例如不同考试间学生的重叠、教室容量限制。
- 软约束:如考试间的时间间隔、较大的考试应该更早安排。

本地搜索启发式设计
关键要素:
- 表示:考试的时间和地点用一组整数数组表示。
- 初始化:随机为每个考试分配时间和教室。
- 目标函数:约束违反的次数。
邻域操作(扰动):
- OP1:随机选择一个考试并重新安排到另一个时间段。
- OP2:随机选择一个考试并换到另一个教室。
- OP3:随机选择一个考试,同时改变其时间和教室。
这些操作可以参数化,例如选择N个事件并应用一个操作。

迭代本地搜索与模拟退火
迭代本地搜索:
- 使用OP3作为邻域操作,只接受改善或不恶化的移动。
模拟退火:
- 初始温度:由初始解的目标值确定。
- 冷却计划:几何冷却,降温系数 (\alpha=0.99)。
- 终止条件:当达到固定的迭代次数或约束违规的数量未改善时停止。
这些方法用于解决考试时间表的优化问题,特别是在复杂约束和大规模问题上表现出的效率和实用性。


这幅图展示了超启发式框架的概念,重点在于如何通过一个称为”域屏障”的抽象层将问题领域中的底层启发式与超启发式策略相结合。
超启发式框架
- 超启发式(Hyper-heuristic):这是一种高层次的问题独立策略,用于管理和控制底层启发式算法。它们主要处理域独立的信息,如候选解的质量变化、底层启发式的数量(人口规模),以及应用启发式的性能和统计数据。
- 域屏障(Domain Barrier):这是一个分隔层,用于区分超启发式操作的高层次决策和具体问题领域的具体实现。这个层使得超启发式能够在多个问题领域中通用,而不需要对每个具体问题进行详尽的定制。
方法选择建设性启发式
- 混合低级启发式(Mix low level heuristics):这种方法涉及选择和组合多种建设性底层启发式算法。目的是利用不同启发式的独特优势来提高解决方案的质量和搜索效率。
这种
框架的主要优势在于其灵活性和广泛适用性,可以应用于多种类型的优化问题,如调度、路由或配置问题等。通过将超启发式作为一个独立于具体问题领域的策略,可以更容易地跨不同类型的问题迁移和应用相同的策略,从而降低开发针对每个新问题的专用算法的复杂性和成本。
在实际应用中,超启发式通常需要调整和优化以满足特定问题的需求,例如选择合适的底层启发式组合、调整域屏障以确保信息有效传递,以及细化超启发式的控制逻辑以提高解决方案的整体质量和效率。
这种框架不仅提供了一种系统化的方法来处理复杂的优化问题,还通过提供一个可扩展的结构来促进算法的创新和改进。在研究和工业应用中,超启发式被视为一种有力的工具,能够处理各种动态和静态问题,适应多变的需求和条件。

这张图展示了一个基于图的超启发式框架(GHH),这是一个使用一组底层建设性图着色启发式的通用框架。这些启发式主要用于排序和解决考试及课程时间表问题。
关键要素解释:
基于图的超启发式(Graph-based Hyper-Heuristics, GHH):这个框架利用图着色原理来解决排程问题,如考试或课程时间表。通过图的方式表示问题,顶点可以代表考试或课程,边则表示约束条件,如同一群学生的考试不能同时进行。
低级启发式(Low Level Heuristics):这些是序列方法,根据分配难度来排序事件。在此框架中,使用了五种图着色启发式,这些启发式有助于决定哪些考试或课程应该先排,以减少冲突和优化资源使用。
- 例如,可以使用之前提到的最大度启发式、最大饱和度启发式等。
- 随机排序策略也可能被包括在内,作为比较或探索解空间的一种方法。
应用领域:此框架特别适用于考试和课程时间表问题,这些问题通常具有复杂的约束和多变需求。通过合理的图着色策略,可以有效地安排时间和资源,确保满足各种硬性和软性约束。
应用效果:
这种基于图的超启发式框架通过将时间表问题视为图着色问题,允许研究者和实践者使用已经在图论中广泛研究的方法来寻求解决方案。这种方法不仅提高了问题解决的效率,还增强了解决方案的适应性和可扩展性,适用于从小规模学校到大型教育机构的多种教育环境。


这张幻灯片介绍了如何将考试时间表问题表示为图着色问题,以及其相关的模型和目标。
考试时间表问题的图表示
问题描述:
- 共有7场考试(e1到e7)。
- 有5名学生(s1到s5),每名学生报名参加不同的考试。
如何模型化:
- 考试作为图的节点。
- 如果两场考试有共同的学生,则这两个节点之间存在边。
- 考虑的示例图中,e1, e2, e3等节点通过边相连,表示学生的考试重叠。
忽略因素:
- 幻灯片提到在这个示例中不考虑教室分配,只关注时间分配。
图着色问题
基本要素:
- 节点:代表考试。
- 边:代表考试之间由于学生重叠的约束。
- 颜色:代表考试时间段。
目标:
- 将颜色(时间段)分配给节点(考试),使得任何相邻的节点(有学生重叠的考试)都不共享同一颜色。
- 尽量减少使用的颜色总数(时间段),从而优化整体考试安排。
应用
通过将考试时间表问题转化为图着色问题,我们可以利用图着色算法来寻找最优或近似最优的解决方案。这种方法允许系统地处理学生的重叠和时间分配的问题,同时尽量减少所需的考试时间段,提高资源的利用效率。这种模型化方法适用于大学和学校等教育机构,可以帮助他们更有效地安排考试时间表。

这张幻灯片展示了一种基于图的超启发式算法中使用禁忌搜索(Tabu Search)的伪代码,并介绍了几种图着色启发式及其配套的排序策略。
禁忌搜索的伪代码解释:
- 初始启发式列表:列出了一组可用的启发式方法 ( h_1, h_2, \ldots, h_k )。
- 禁忌列表:用于避免算法陷入局部最优,记录最近访问的启发式。
- 迭代过程:
- 每次迭代中,从启发式列表中选择两个启发式进行组合,如果这个组合不在禁忌列表和失败列表(记录导致不可行解的启发式组合)中,则进行尝试。
- 使用所选的启发式方法 ( h_j ) 构建解决方案。
- 如果找到可行解且该解的成本小于当前最佳成本,则更新最佳解。
- 否则,将启发式方法加入失败列表。
- 控制禁忌列表的大小,保证其不超过9个元素。
- 最终步骤:对得到的最佳解进行最深层次下降搜索(Deepest Descent),以进一步优化解。
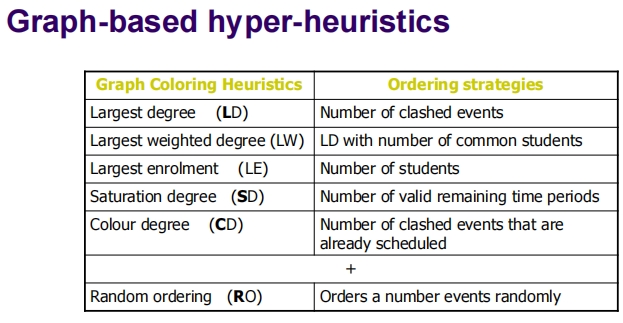
图着色启发式及排序策略:
图着色启发式:
- 最大度(LD):选择最多邻居的节点。
- 加权最大度(LW):考虑节点邻居的权重。
- 最大注册量(LE):选择学生数最多的考试。
- 饱和度(SD):选择与最多已着色邻居相连接的节点。
- 颜色度(CD):选择已经排定的且冲突最多的考试。
- 随机排序(RO):随机选择事件进行排序。
排序策略:
- 根据事件冲突数、共同学生数、剩余有效时间段数量以及已安排事件的冲突数来排序。
这种方法的优势在于它结合了多种启发式策略,通过动态调整使用的策略,增加了解决复杂调度问题的灵活性和有效性。此外,通过禁忌列表和失败列表的运用,算法能够避免重复探索无效或次优的路径,从而提高搜索效率。
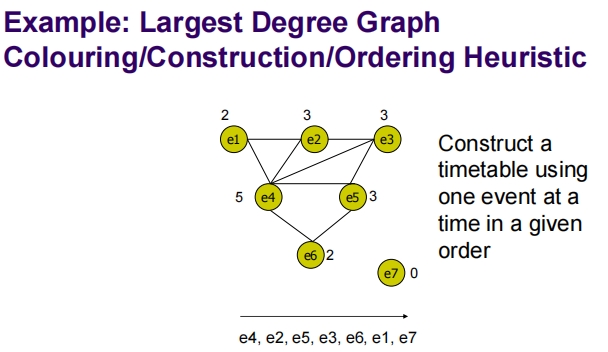
这幅图提供了两个示例,展示了如何使用最大度启发式和最大注册量启发式来构建考试时间表。
最大度图着色/构建/排序启发式
在这个示例中,各个考试(事件)的节点按它们的连接度(与其他事件的连接数)来排序:
- 节点及其度:e4 (5), e2 (3), e3 (3), e5 (3), e6 (2), e1 (2), e7 (0)
- 排序:根据度的大小降序排列,得到的顺序为 e4, e2, e5, e3, e6, e1, e7。
这种方法首先处理连接最多的考试,旨在优先解决可能引起最多约束冲突的考试,以此来最小化整体冲突。
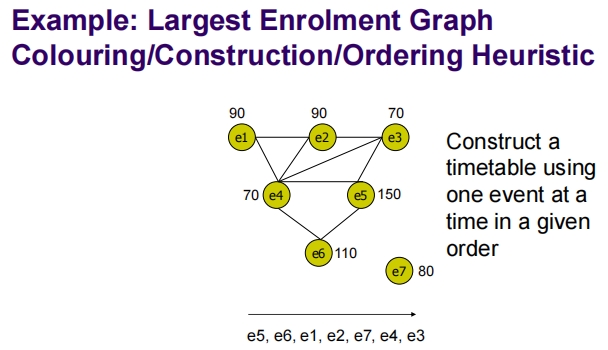
最大注册量图着色/构建/排序启发式
在这个示例中,考试根据学生注册量(即参加考试的学生数量)来排序:
- 节点及其注册量:e5 (150), e6 (110), e1 (90), e2 (90), e3 (70), e4 (70), e7 (80)
- 排序:根据注册量降序排列,得到的顺序为 e5, e6, e1, e2, e7, e4, e3。
这种方法优先处理参与人数最多的考试,其目的是尽快安排那些影响最大学生群体的考试,从而尽可能减少因时间冲突带来的影响。
启发式的选择和应用
这两种启发式提供了不同的优先级策略,适用于具体问题的特定需求。选择哪一种启发式取决于问题的具体约束和优化目标。在实际应用中,可能需要根据问题的规模和复杂性调整或结合多种启发式方法,以达到最优解。通过逐个安排每个事件,并检查与已安排事件的时间冲突,这些方法帮助减少时间表中的总冲突数。
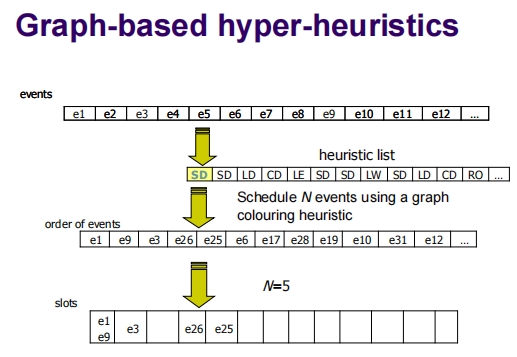
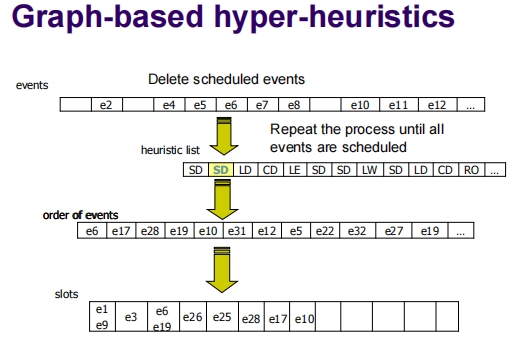
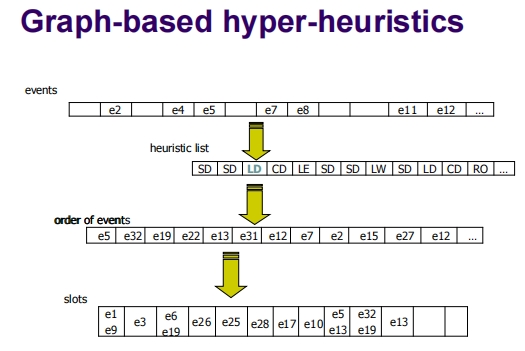
这些幻灯片展示了如何使用基于图的超启发式方法来为一系列事件进行时间安排。这个过程分为几个步骤,包括选择适当的启发式策略,为事件排序,然后根据这种排序将事件分配到时间槽中。
步骤解析
事件和启发式列表:
- 每个事件(如e1, e2, e3等)被列出。
- 启发式方法的列表也被制定,包括饱和度(SD)、最大度(LD)、颜色度(CD)等,这些方法用于确定事件的处理顺序。
事件排序:
- 使用选择的启发式方法,为事件确定一个处理顺序。例如,可能首先使用饱和度启发式,然后是最大度启发式,再接着是颜色度启发式等。
- 这些启发式方法基于各种图的属性(如节点的连接度、节点的颜色饱和度等)来优化事件的排序。
分配到时间槽:
- 根据事件的排序,事件被一一放置到时间槽中。每次放置过程中,都会尝试最小化时间槽的使用和避免冲突。
- 如图所示,按照排序,选定的事件被安排到特定的时间槽中。
迭代过程:
- 一旦一批事件被安排后,这些事件就从总列表中删除。
- 重新应用启发式方法为剩余的事件重新排序并分配到新的时间槽中。
- 这个过程重复进行,直到所有事件都被安排完毕。
示例
- 在第一个示例中,根据启发式策略安排了五个事件(e1, e3, e26, e25, e9)到时间槽中。
- 第二个和第三个示例中继续显示了后续的迭代过程,事件如e6, e17, e28等被安排到新的时间槽中。
这种方法有效地展示了如何动态利用不同的启发式策略来优化事件的时间安排,这对于解决复杂的调度问题(如考试时间表、会议安排等)非常有用。通过这种方式,可以确保时间表的高效利用,同时减少冲突。

这张幻灯片介绍了图基超启发式(Graph-based Hyper-heuristics, GHH)的应用,特别是使用禁忌搜索来优化启发式列表,以及比较不同的高级搜索策略。
禁忌搜索在超启发式中的应用
禁忌搜索(Tabu Search):
- 在高层级进行操作。
- 邻域操作:在启发式列表中随机改变两个启发式。
- 目标函数:评估对应启发式列表构建的解决方案的质量。
- 禁忌列表:阻止对相同启发式列表的重复访问。
其他测试的高级搜索策略:
- 最陡下降(Steepest Descent)
- 可变邻域搜索(Variable Neighbourhood Search) - 表现最佳。
- 迭代最陡下降(Iterated Steepest Descent)
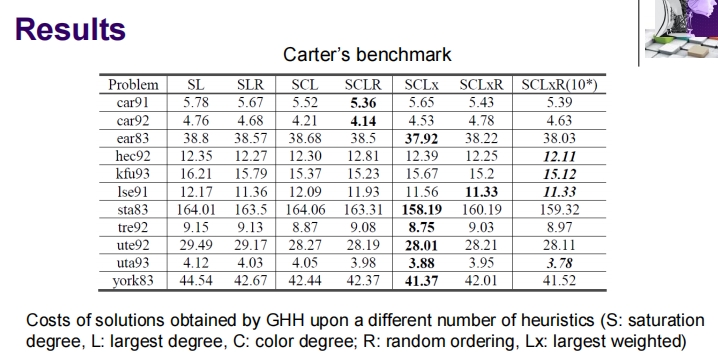
实验结果
- 数据集:使用了Carter的基准数据集,这是一个经典的测试集,用于评估教育时间表问题的解决策略。
- 性能指标:展示了不同启发式组合(如饱和度、最大度、颜色度、随机排序、最大权重)对问题解决方案的成本影响。
- 结果对比:
- 每个问题的解决方案成本使用了不同启发式组合来计算。
- 表格列出了不同启发式组合在各个问题上的表现,如SL(饱和度最低)、SLR(饱和度最低、随机排序)等。
结论
幻灯片提供的信息表明,通过使用图基超启发式和禁忌搜索等高级搜索策略,可以有效地提高解决复杂调度问题的能力。可变邻域搜索在这些策略中表现最佳,表明对于某些类型的问题,改变搜索邻域可以极大提高搜索效果。这些策略和技术的有效结合为解决实际应用中的时间表问题提供了有力的工具。
Generation Hyper-heuristics

这张幻灯片详细介绍了遗传编程(Genetic Programming, GP)的概念、挑战和理由。
遗传编程 (GP) 的概念
遗传编程是一种自动化的计算方法,旨在从高层次的问题描述自动创建出能解决该问题的计算机程序。这一过程模拟自然进化的原理,通过迭代过程不断地在程序的“种群”中选择、复制、变异和重组,以产生新一代的程序,从而优化程序的性能。
遗传编程的挑战
遗传编程面临的主要挑战是“让计算机去做需要做的事情,而不必告诉它具体怎么做”。这意味着系统必须能够自行理解问题并找到解决方案,而不是依赖于详细的指令。

为什么选择遗传编程?
自然表达方式:对于许多机器学习和人工智能问题,最自然的解决方案表示形式是计算机程序。这是因为程序能够灵活地表达复杂的、动态变化的数据结构和操作,这在使用固定长度的字符串或其他静态数据结构时难以实现。
解决问题的能力:遗传编程可以解决固定格式难以应对的问题,因为它可以动态调整解决方案的结构,更好地适应问题的需求。
解析树(Parse Tree):在遗传编程中,程序通常用解析树来表示。解析树是一种树形数据结构,可以有效地表示和修改程序代码,非常适合用于遗传算法的操作。
遗传编程作为一种强大的编程范式,能够应用于多种领域,如符号回归、逻辑回归、自动设计、自动编程等,特别是在解决那些传统编程方法难以处理的复杂问题时显示出其独特的优势。通过这种方式,可以发掘出新的、有效的算法和程序,进而推动人工智能领域的发展。

这张幻灯片介绍了遗传编程(Genetic Programming, GP)在各种现实世界应用中的一些精选示例。遗传编程作为一种强大的算法,其主要优势在于能够自动生成解决复杂问题的程序,特别是在那些传统编程方法难以应对的领域。下面是一些应用实例:
自动化设计机电系统(由美国国家科学基金会支持):
- 利用遗传编程来创建或优化机电系统的设计,使系统更高效和适应性更强。
气候学:
- 估计大气与海冰之间的热通量,建模全球温度变化。
- 这种应用利用GP模型复杂的环境系统,并预测其变化,对于理解和应对气候变化至关重要。
临床决策支持系统在眼科学中的应用:
- 在眼科领域,遗传编程被用来支持临床决策,例如自动诊断眼部疾病或优化治疗策略。
集装箱装载优化:
- 优化集装箱的装载方式,以最大化空间利用率和减少运输成本。
调度和时间表编制:
- 遗传编程可以解决复杂的调度和时间表问题,例如学校课程表的制定或大型工厂的生产调度。
机器学习:
- 在机器学习领域,GP用于自动化生成特征、模型或整个预测算法。
车辆路线规划:
- 优化物流和配送中的车辆路线,以减少旅行时间和燃料消耗。
这些应用显示了遗传编程在各种领域的广泛适用性和有效性,尤其是在需要创造性解决方案和自动化设计决策的场景中。遗传编程通过模拟自然选择的原理,能够探索大量潜在的解决方案,找到最适合特定问题的程序,这使得它在解决复杂的优化和设计问题中尤为有价值。


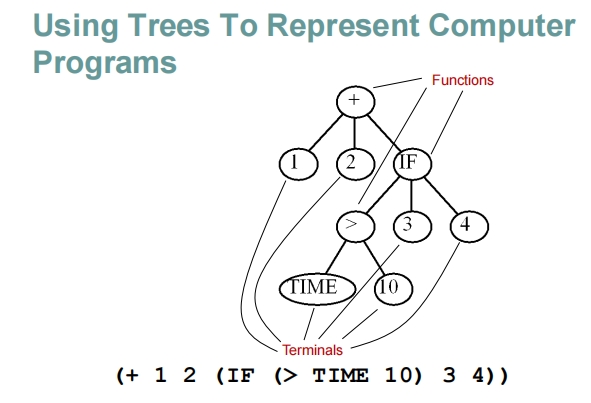
这段C语言代码中定义的函数 foo 根据输入的 time 计算一个值。下面是该函数行为的分析和预期输出:
函数分析
- 函数接收一个整数参数
time。 - 它声明了两个整数变量,
temp1和temp2。 - 如果
time大于 10,temp1设为 3。 - 否则,
temp1设为 4。 - 然后计算
temp2为temp1 + 1 + 2。 - 函数返回
temp2的值。
当 time 从 0 到 14 变化时的预期输出
当
time为 10 或更小时:temp1设置为 4。temp2计算为4 + 1 + 2 = 7。- 因此,函数返回 7。
当
time大于 10 时:temp1设置为 3。temp2计算为3 + 1 + 2 = 6。- 因此,函数返回 6。
每个值从 0 到 14 的输出
- 对于 time = 0 到 10:输出为 7。
- 对于 time = 11 到 14:输出为 6。
这个函数明确展示了基于输入的条件逻辑,并且根据输入是否大于 10 有两个不同的输出值。

这张幻灯片介绍了遗传编程(Genetic Programming, GP)中的遗传操作。遗传编程是一种进化算法,包含以下主要的算法组成部分:
随机生成初始解的种群:
- 在遗传编程的开始,随机生成一组可能的解(程序),作为初始种群。
遗传交叉:
- 选取两个有前途的解(程序),通过遗传交叉操作生成新的可能解。交叉操作通常涉及在两个程序的相应部分之间交换信息,从而创造出含有两个父本特征的新程序。
突变:
- 对有前途的解进行突变,以创造新的可能解。突变操作可能是随机改变程序中的某个部分,比如改变一个操作符或者插入一个新的函数调用,目的是探索解空间中未被现有种群覆盖的区域。
这些操作共同作用,使得程序的种群能够进化,逐步改善解决特定问题的能力。通过不断的迭代这些遗传操作,遗传编程旨在发现效率高、性能好的程序,从而解决复杂的问题。
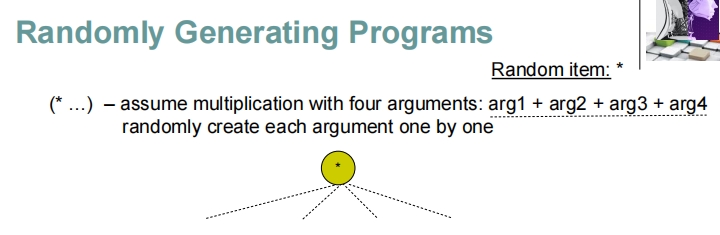
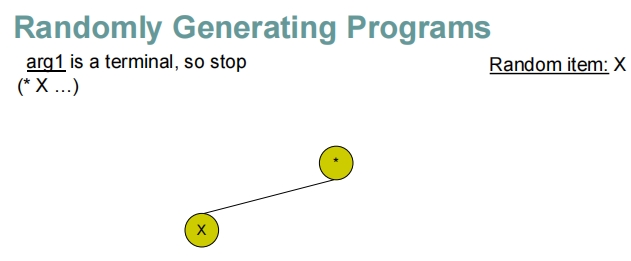
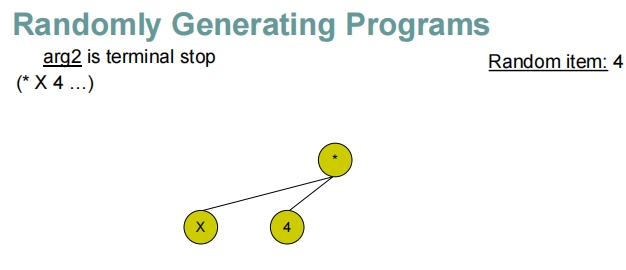
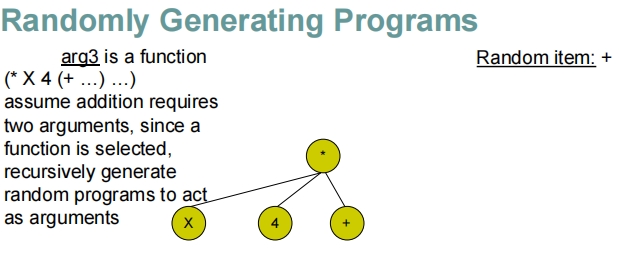
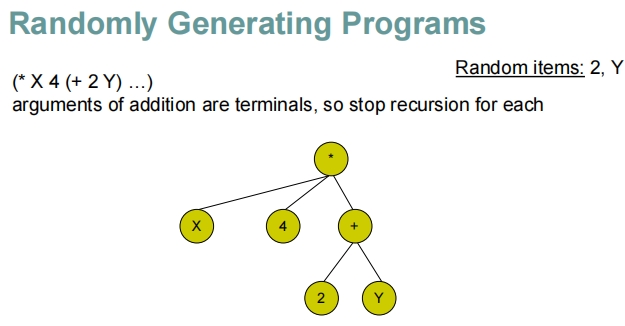
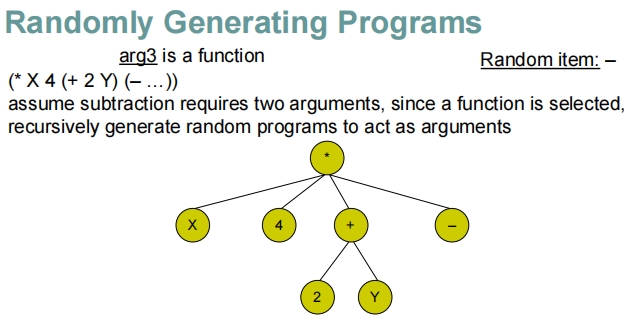
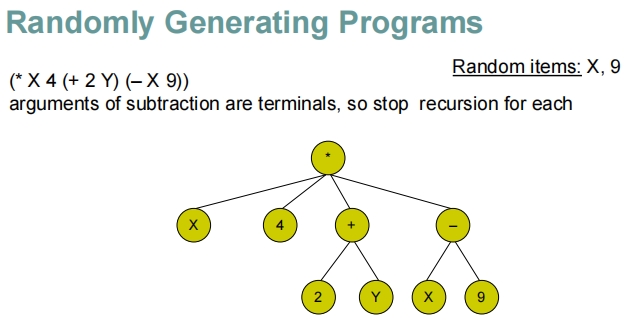
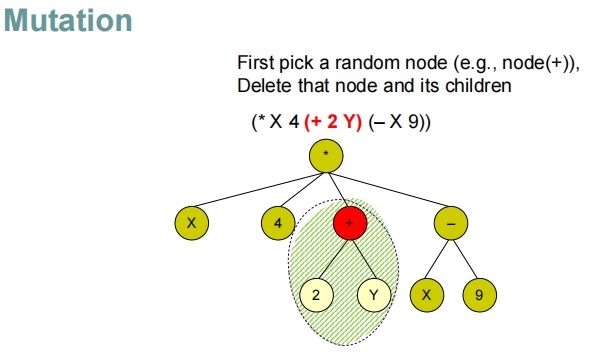
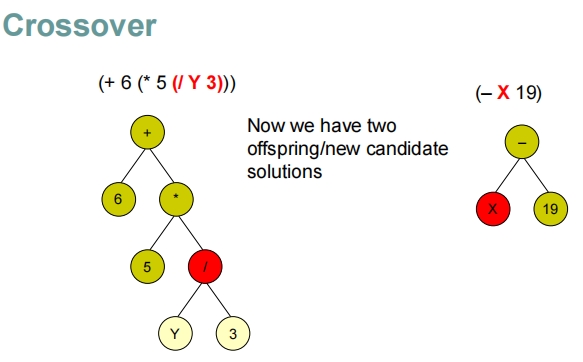
这些幻灯片展示了在遗传编程中随机生成程序的过程,特别是如何通过递归地构建表达式树来生成程序。
随机生成程序的步骤解析
初始化:
- 随机选择一个运算符(如乘法
*)作为根节点。
- 随机选择一个运算符(如乘法
生成参数:
- 对于根节点的每个参数位置,随机决定是放置一个终端(如变量
X或常数4)还是另一个函数(如加法+或减法-)。 - 如果选择了函数,将递归执行此步骤,为该函数生成参数。
- 对于根节点的每个参数位置,随机决定是放置一个终端(如变量
递归构建:
- 每当选择函数作为参数时,递归地为该函数的参数生成新的子树。
- 当决定使用终端作为参数时,递归停止。
完整表达式的构建:
- 这个过程最终生成一个完整的表达式树,其中包含多层嵌套的函数和终端。
示例
乘法函数:
- 例如,根节点为乘法
*,它的参数可能是变量X、常数4,以及其他通过加法或减法生成的表达式。 - 加法
+可能连接常数2和变量Y。 - 减法
-可能从变量X中减去常数9。
- 例如,根节点为乘法
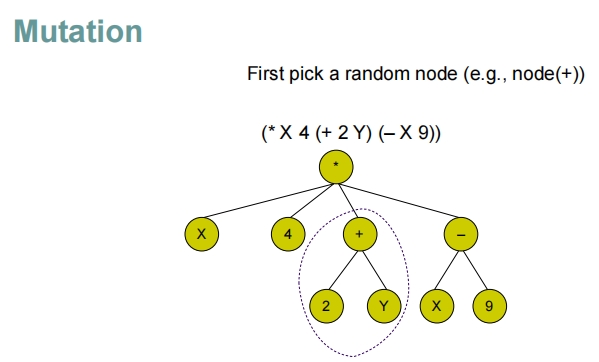
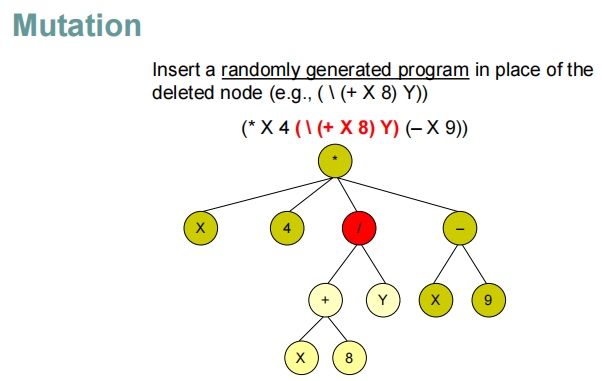
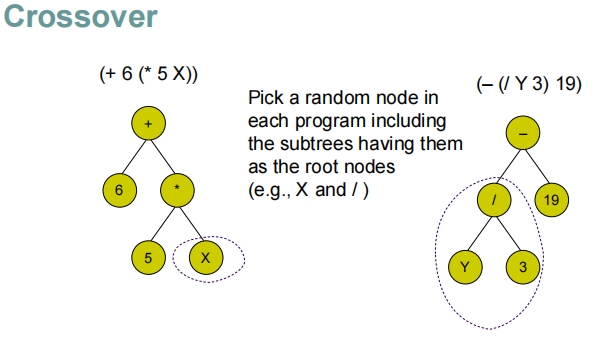
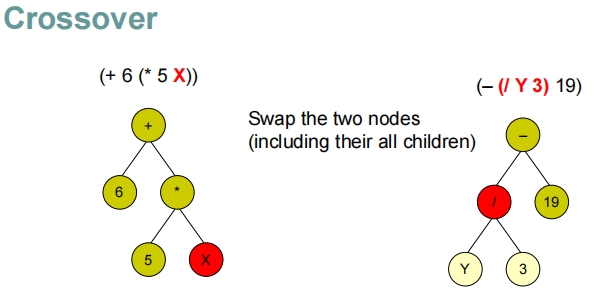
交叉和突变操作:
- 交叉:选取两个程序的随机节点(包括其子树),并交换这些子树,生成新的程序候选。
- 突变:在一个程序的随机节点进行修改,如改变节点的运算符,或用新生成的子树替换现有子树。
结果
- 通过这种方式,遗传编程不仅能够探索解空间中的现有点,还能发现新的可能性,进而优化和改进程序。这种方法使得程序能够适应复杂的问题环境,通过自然选择和遗传变异机制持续进化。
这两张幻灯片介绍了超启发式框架及其在遗传编程中的应用。超启发式是一种高级别的启发式方法,用于控制和指导底层启发式的选择和应用。下面是详细的解释:
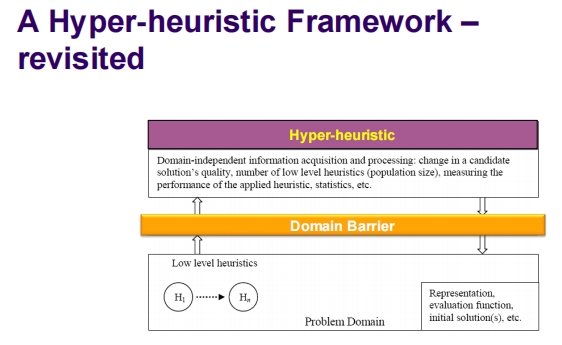
超启发式框架重访
超启发式层:
- 负责收集和处理域独立的信息,例如候选解的质量变化、底层启发式的数量(种群大小)、应用启发式的性能、统计数据等。
域屏障:
- 作为一个抽象层,它隔离了超启发式和问题域的具体实现。这使得超启发式能够在不同的问题域之间进行通用和灵活的应用。
底层启发式:
- 这些是直接与问题域相关的启发式方法,包括具体问题的表示、评估函数、初始解等。
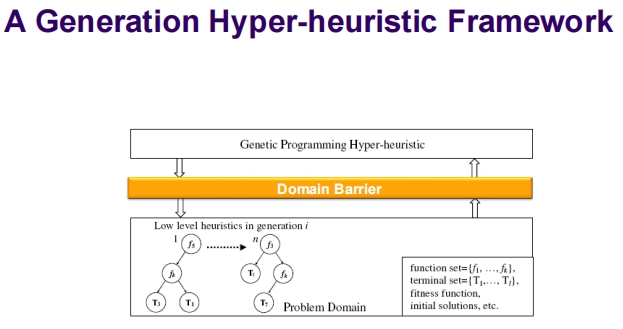
生成型超启发式框架
遗传编程超启发式:
- 该框架利用遗传编程的技术来生成和优化启发式。通过模拟自然选择和遗传机制,逐代进化出更适应问题的启发式。
域屏障:
- 同样存在于这个框架中,确保超启发式的通用性和可迁移性。
底层启发式在生成 i:
- 代表每一代中遗传编程产生的底层启发式集合。这些启发式通过遗传编程的操作(如选择、交叉和突变)不断进化。
问题域组件:
- 包括函数集、终端集、适应度函数、初始解等,这些是遗传编程在特定问题域内操作的基础。
这些框架展示了如何将超启发式方法应用于复杂问题解决中,特别是如何通过遗传编程来动态生成和优化用于具体问题解决的启发式。通过这种方法,可以在保持高度灵活性和适应性的同时,提高问题解决的效率和效果。
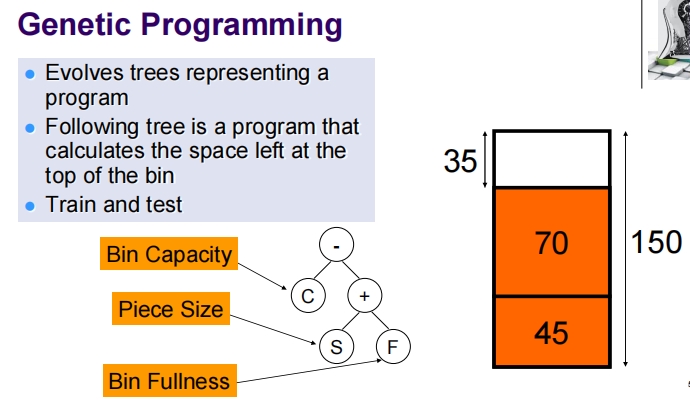
Genetic Programming for Packing

这张幻灯片介绍了一维离线装箱问题(1D Offline Bin Packing),这是一个标准的NP难题。
一维离线装箱问题简介:
问题定义:
- 任务是将一组大小为 (s_i)(对于 i = 1, …, n)的物品打包到若干个容量为 (C) 的箱子中。
- 每个物品的大小都是整数,并且每个物品的大小 (s_i) 满足 (1 \leq s_i \leq C)。
目标:
- 确保每个箱子的总装载量不超过其容量 (C)。
- 使用尽可能少的箱子来装载所有物品。
挑战:
- 一维离线装箱问题是一个NP难题,意味着没有已知的多项式时间算法可以解决所有实例。
解决策略:
- 在解决此问题时,通常采用各种启发式算法,如最先适应(First Fit)、最佳适应(Best Fit)等,这些算法尽管不能保证找到最优解,但在实践中表现出了相对较好的性能。
- 此外,也可以通过更复杂的算法如遗传算法、线性编程或者混合整数编程等来寻求更接近最优的解决方案。
- 遗传算法等进化算法特别适用于此类问题,因为它们可以通过模拟自然选择的过程来探索解空间,不断优化候选解决方案。
这类问题在工业和商业领域有广泛的应用,例如在仓库物流、货运装载以及资源优化等方面。通过有效的解决方案,可以显著减少资源的浪费,提高效率。


这幅幻灯片展示了一系列关于装箱和背包问题的实验及其结果。实验设计旨在对比来自18篇论文的结果,并涵盖了一维、二维和三维的问题。
实验概述:
实验对比:
- 从18篇研究论文中比较了结果。
实验分类:
- 一维装箱问题:涉及两组实例。
- 二维背包和装箱问题:涉及十组实例。
- 三维背包和装箱问题:涉及六组实例。
结果概览:
分析:
- 一维装箱问题的结果显示,在大部分实例中没有明显改进,甚至有些情况下效果更差。
- 二维和三维背包问题的结果则表现出在某些实例中显著的改进,尤其是Ep340实例在三维背包问题中改进了13.0%。
这些实验表明,在更高维度的问题中,可能通过优化算法和策略来获得更好的改进效果。这些数据提供了深入了解不同维度问题解决策略效率的基础,并可以用于进一步的研究和算法开发。

这张幻灯片介绍了遗传编程(GP)超启发式在装箱问题中的应用,特别是它如何为一维(1D)、二维(2D)和三维(3D)的装箱和背包问题提供一种更通用的解决方法。
GP超启发式在装箱问题中的应用:
通用方法:
- GP超启发式为不同维度的装箱和背包问题提供了一种统一的方法。这种方法的优势在于它能够适用于多种问题类型,而无需为每种问题单独设计或调整算法。
保持解决方案质量:
- 尽管方法具有高度的通用性,但它能够在不牺牲解决方案质量的前提下,实现这一点。这意味着在解决各种问题时,可以保持或甚至提高解决方案的效率和有效性。
优势分析:
- 灵活性:能够处理各种大小和复杂度的问题,不受限于特定的问题结构。
- 效率:通过遗传算法的演化机制,能够在较大的解空间中快速寻找到高质量的解决方案。
- 可扩展性:适用于从简单的一维问题到复杂的三维问题,这种扩展性使得GP超启发式特别适合处理实际应用中的多变和复杂需求。
这种方法的成功展示了遗传编程在解决具有高度复杂性和变异性问题时的强大潜力。通过自然选择和遗传机制来不断优化解决策略,GP超启发式为解决各种装箱和背包问题提供了一种高效的工具。


这两张幻灯片提供了关于超启发式和遗传编程超启发式的总结,特别是它们在搜索策略和性能影响方面的应用。
第一部分:超启发式总结
搜索方法的多样性:
- 搜索方法由不同的组件、算法配置或参数设置组成,这些元素的不同组合常常导致性能表现的差异。
元启发式与超启发式:
- 元启发式在解空间中搜索解决方案。
- 超启发式(可能本身是一种元启发式)在低级启发式的空间中进行搜索。
超启发式的选择:
- 可以使用选择性超启发式来混合扰动型和构建型低级启发式。
第二部分:遗传编程超启发式总结
低级启发式的选择:
- 在超启发式框架中使用的低级启发式的选择显著影响其性能。
遗传编程超启发式:
- 用于构建启发式或启发式组件。
- 这些通常以训练和测试的方式操作。
- 在选定的样本实例上训练可能需要较长时间,而在未见实例上的应用通常较快。
性能评估:
- 通过遗传编程生成的每棵树可以使用指标评估,该指标显示其在构建高质量解决方案方面的效果,如样本问题实例上解决方案的平均质量。
这些总结强调了超启发式在解决复杂问题中的实用性,尤其是遗传编程超启发式如何有效地生成和优化解决策略。通过这种方法,可以提高算法在各种情境下的适应性和效率,特别是在处理大规模和多变问题时。这种灵活性和高效性使得超启发式特别适用于需要动态调整和优化算法性能的领域。
Lecture09 (Advanced Topics)


这张图片介绍了两种1D装箱问题:离线装箱问题(Offline Bin Packing)和在线装箱问题(Online Bin Packing)。
1D 离线装箱问题:
- 目标:将一组物品尺寸 ( s_i ),其中 ( i = 1, \ldots, n ),装入固定容量为 ( C ) 的箱子中。
- 要求:
- 物品的尺寸为整数,且 ( s_i ) 的取值在 1 到 ( C ) 之间。
- 尽量减少使用的箱子数量。
- 确保不超过箱子的容量。
- 这是一个标准的NP-hard问题,解决起来非常具有挑战性。
1D 在线装箱问题:
- 目标:按照物品到达的顺序,一个一个地将物品尺寸 ( s_i ),其中 ( i = 1, \ldots ),装入固定容量为 ( C ) 的箱子中。
- 要求:
- 物品尺寸同样为整数,且 ( s_i ) 的取值在 1 到 ( C ) 之间。
- 尽量减少使用的箱子数量,同时最大化箱子的平均填充率。
- 同样需要确保不超过箱子的容量。
- 在线装箱问题比离线问题更加复杂,因为决策必须在物品到达时即刻做出,而且无法预知后续物品的大小。
这两种问题都广泛应用于物流、计算机存储管理等领域,解决方法包括各种启发式算法和近似算法,用于找到实用的近似解。

这张图片介绍了解决一维装箱问题时两种标准启发式方法:首次适应(First-fit)和最佳适应(Best-fit)。
首次适应(First-fit)启发式方法(BP-FF):
- 在这种方法中,物品按它们到达的顺序进行放置。
- 对于每个新到达的物品,它会被放置在第一个能够容纳它的箱子中(即编号最小的箱子)。
- 如果当前所有打开的箱子都不能容纳这个物品,就会开启一个新的箱子。
最佳适应(Best-fit)启发式方法(BP-BF):
- 在这种方法中,物品同样按到达的顺序进行放置。
- 对于每个新到达的物品,它会被放置在能够容纳它的情况下剩余空间最少的箱子中。
- 如果没有现有的箱子可以容纳这个物品,同样会开启一个新的箱子。
图中展示了一个例子,其中 ( S = {4, 8, 5, 1, 7, 6, 1, 4, 2, 2, \ldots} ) 是物品的大小序列,每个箱子的容量 ( C = 10 )。可以看到,不同的启发式方法会导致不同的箱子使用策略和效率。
这些方法的优点是实现简单且计算速度快,但它们不保证找到最优解,只能提供可行的近似解。在实际应用中,根据具体情况选择合适的启发式方法是很重要的。
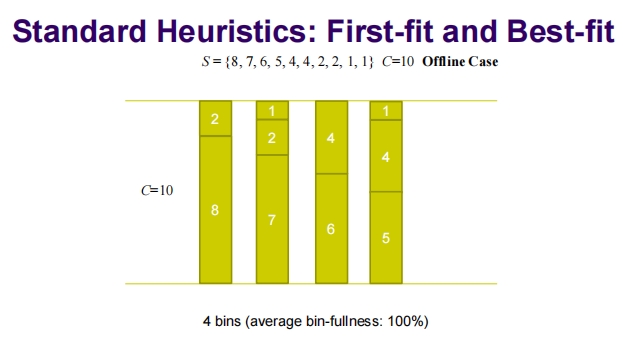

这两张图片比较了使用首次适应(First-fit)启发式方法在离线和在线情况下的一维装箱问题的效果。
离线情况:
- 物品序列为 ( S = {8, 7, 6, 5, 4, 4, 2, 2, 1, 1} ),每个箱子的容量为 ( C = 10 )。
- 使用了4个箱子,每个箱子都恰好装满,平均装箱满度为100%。
- 这表明在离线情况下,首次适应方法能够非常有效地利用空间,达到最优的装箱方式。
在线情况:
- 物品序列为 ( S = {4, 8, 5, 1, 7, 6, 1, 4, 2, 2, \ldots} ),每个箱子的容量同样为 ( C = 10 )。
- 使用了5个箱子,其中一个箱子未装满,平均装箱满度为80%。
- 这表明在在线情况下,由于物品是按照它们到达的顺序被放置,无法事先知道所有物品的信息,导致装箱效率下降。
总的来说,这两张图表展示了离线模式下能更好地计划和优化装箱,而在线模式则受到物品到达顺序的限制,通常会导致更低的空间利用率和更高的箱子使用数。这种对比展示了不同场景下策略的性能差异,对于设计更有效的装箱策略具有重要意义。

这张图片介绍了“指数策略”(Index Policies),这是一种在决策过程中使用的策略,通常应用于资源分配、任务调度等优化问题。下面是关于指数策略的一些关键点:
定义与原理:
- 指数策略是指为每个选择项独立地赋予一个分数或“指数值”(index value)。
- 在决策时,选择具有最高指数值的选项。
- 如果存在指数值相同的情况,还需要一个规则来打破平局。
应用场景与优势:
- 虽然指数策略是一个特殊情况,但在某些情况下它们可以是最优的,或者至少非常有效。
- 这种策略的优势在于其简单性和独立性,使得每个选项可以单独评估,而不必担心其他选项的影响,这在计算上是非常高效的。
举例:
- 在资源分配问题中,每个任务可能根据其紧迫性、资源需求等因素被赋予一个指数值。系统会优先处理指数值最高的任务。
- 在装箱问题中,每个物品的指数值可能是基于其大小与剩余容量的比率计算的,以此来优化箱子的使用效率。
指数策略的一个关键优势是它们通常易于实现,并且能快速做出决策,这在需要实时或近实时决策的应用中尤为重要。不过,这种策略也可能忽略了一些长期影响或多步骤策略中的相互依赖性。

这张图片介绍了用于1D在线装箱问题的指数策略(Index Policies)。以下是关于这种策略的详细解释:
基本概念:
- r:箱子的剩余容量(残余空间)。
- s:物品的大小。
- 为每个箱子赋予一个分数,这个分数是基于函数 ( f(r, s) ) 计算的,其中 ( r ) 是箱子的剩余容量,( s ) 是待放置物品的大小。
决策过程:
- 当一个新的物品到来时,它将被放置在具有最大 ( f(r, s) ) 值的箱子中。
- 这样做是为了最大化某种效益,比如最大化箱子的填充率或最小化空间浪费。
处理平局情况:
- 如果有多个箱子的 ( f(r, s) ) 值相同,那么会使用首次适应(First-fit, FF)策略来打破平局。
- 具体来说,会将物品放置在序号最小的(或最早创建的)拥有最佳得分的箱子中。
这种指数策略为在线装箱问题提供了一个实用的解决方案,允许即时决策,并且可以适应随时到来的新物品。这种方法特别适用于物流和仓储管理,其中物品的到达时间不确定,且需要即时决策以优化空间使用。通过合适地选择和调整评分函数 ( f ),可以显著影响整体的装箱效率和性能。
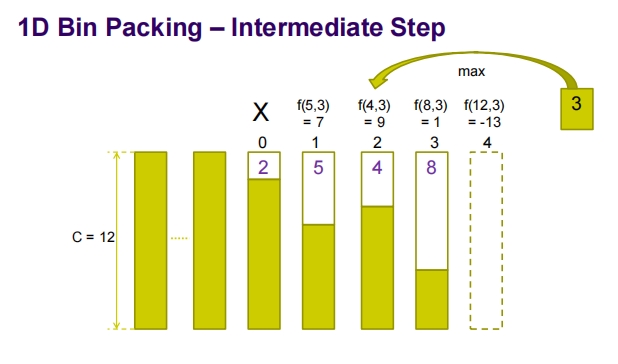
这张图片展示了1D在线装箱问题中的一个中间步骤,使用了指数策略来决定新物品应该放在哪个箱子中。
在这个例子中,我们看到:
箱子容量:每个箱子的容量是 ( C = 12 )。
箱子状态:
- 箱子 0 有 2 单位的空间占用。
- 箱子 1 有 5 单位的空间占用。
- 箱子 2 有 4 单位的空间占用。
- 箱子 3 有 8 单位的空间占用。
新物品尺寸:新物品的大小为 3 单位。
评分函数 ( f(r, s) ):这个函数基于箱子剩余容量 ( r ) 和物品大小 ( s ) 来计算得分。
- 对于箱子 0,( f(10, 3) = 7 )(因为箱子0剩余容量为 ( 12-2=10 ))。
- 对于箱子 1,( f(7, 3) = 9 )(因为箱子1剩余容量为 ( 12-5=7 ))。
- 对于箱子 2,( f(8, 3) = 1 )(因为箱子2剩余容量为 ( 12-4=8 ))。
- 对于箱子 3,( f(4, 3) = -13 )(因为箱子3剩余容量为 ( 12-8=4 ),可能因为物品尺寸与剩余容量接近造成得分低或有惩罚因子)。
决策:
- 选择最高分 ( f(r, s) ) 的箱子放置新物品。在这种情况下,箱子 1 的得分最高,所以新物品将被放置在箱子 1 中。
这个过程演示了如何通过计算每个箱子对于特定物品的得分来做出最优决策,以实现更高的空间利用率和更少的箱子使用。这种方法在在线场景中特别有用,因为它允许系统在不知道未来物品信息的情况下做出最优的即时决策。

1D Online Bin Packing 基本概念
新箱子总是可用(开放):
- 这意味着无论何时有新物品到来,总可以开启一个新的空箱子来放置物品。
箱子的关闭条件:
- 如果一个箱子的剩余空间小于任何一个物品的大小,这个箱子就会被认为是关闭的,不能再放入新物品。
需要一个好的“策略”:
- 需要一种方法或策略来决定新到达的物品应该被放置在哪一个开放的箱子中。这个策略的目的是优化总体的箱子使用,比如最小化总箱数或最大化箱子的填充率。

1D Online Bin Packing 潜在的通用方法
新物品到达时的处理:
- 当一个新的物品到达时,需要检查当前所有开放的箱子。
- 使用所有开放箱子中的剩余空间集合来决定放置新物品的位置。
方法的挑战:
- 这种方法在实际操作中可能既困难又昂贵,因为需要实时评估多个箱子的剩余空间,并从中选择最优的一个。这需要复杂的计算,尤其是在箱子数量很多的情况下。
综合解释
这两张图片展示了在线装箱问题的复杂性和处理新物品的需求。有效的在线装箱策略(如首次适应、最佳适应、指数策略等)可以帮助减轻决策过程的复杂性,并提高整体的效率。每种策略都有其优势和局限,选择合适的策略取决于具体的应用场景和性能要求。这个问题的挑战在于如何在接收到新物品的信息时快速而准确地作出决策,以最大化空间利用率和最小化所需的箱子数量。

这张图片介绍了一种通过遗传编程(Genetic Programming, GP)自动生成启发式评分函数的方法,具体用于解决装箱问题中的决策问题。以下是关于这个方法的详细解释:
主要内容
在搜索方法中使用评分函数:
- 在许多搜索和优化算法中,评分函数(或称“指数函数”)用于帮助做出选择。
- 评分函数的设计往往难以手工完成,因此存在将这一过程自动化的需求。
遗传编程(GP)方法:
- GP是一种通过模拟自然选择和遗传学原理来解决问题的方法,它可以自动地进化出算法或函数。
- 在这个场景中,GP被用来发展和优化算法中的评分函数 ( f(r, s) ),其中 ( r ) 是箱子的剩余空间,( s ) 是待放置物品的大小。
评分函数的表示:
- 通过遗传编程生成的评分函数被表示为算术函数树。这种表示方法允许函数通过遗传操作(如交叉和突变)在进化过程中自然变化。
功能和目标:
- 这种方法自动创建的函数目的是至少匹配或超过传统的首次适应(First Fit, FF)和最佳适应(Best Fit, BF)策略的效果。
- 通过不断优化这些函数,可以发展出更高效或更适合特定应用场景的启发式评分函数。
应用和优势
- 自动化和优化:自动生成启发式评分函数减少了人工干预,降低了设计复杂启发式策略的难度和时间成本。
- 灵活性和适应性:遗传编程生成的函数可以适应各种不同的约束和目标,使得它们在多变的实际应用场景中更加有效。
- 性能提升:通过自然选择机制,只有最有效的函数才会被保留和复制,从而提高了整体算法的性能。
总结
使用遗传编程自动生成启发式评分函数是一种先进的技术,它利用生物进化的原理来解决复杂的优化问题,特别是在需要处理大量数据和变量的情况下,这种方法显示出了巨大的潜力和优势。
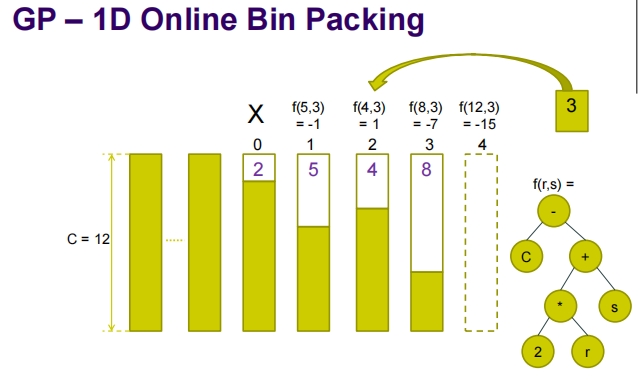
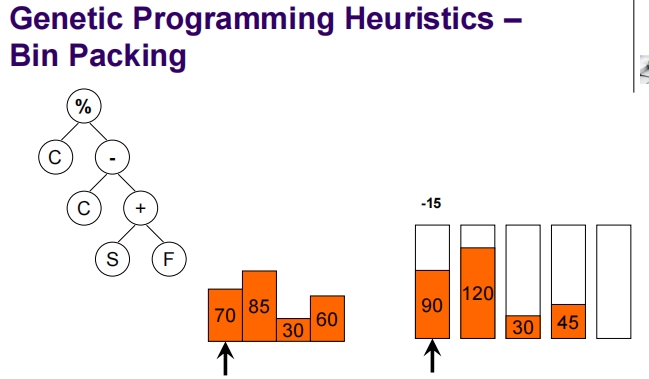
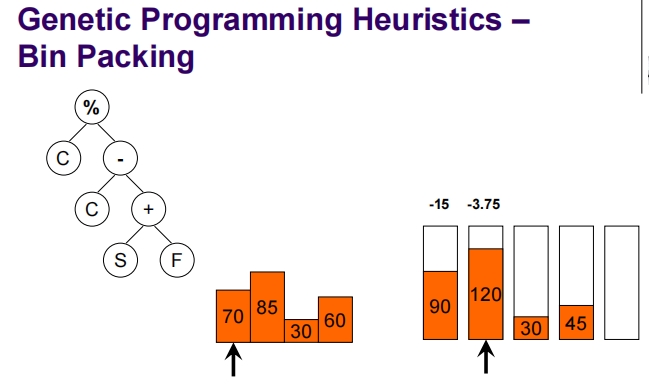
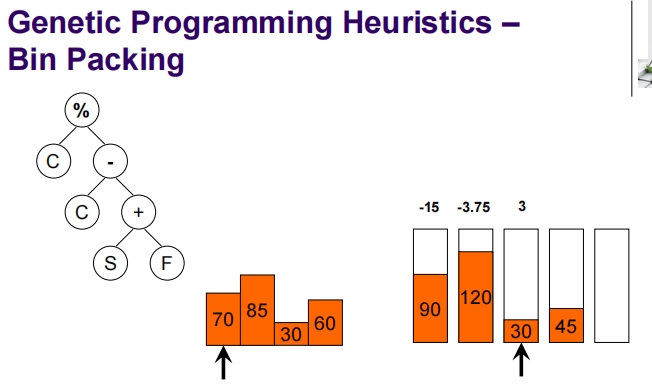
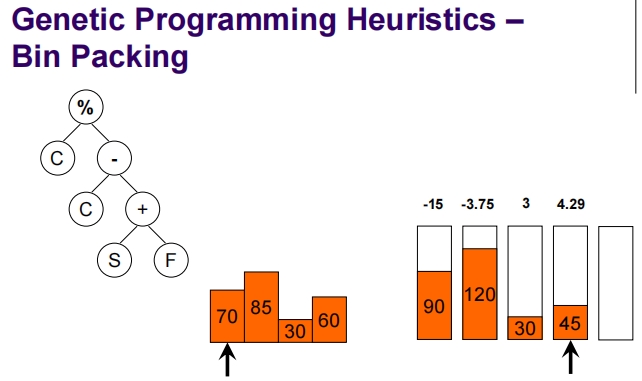
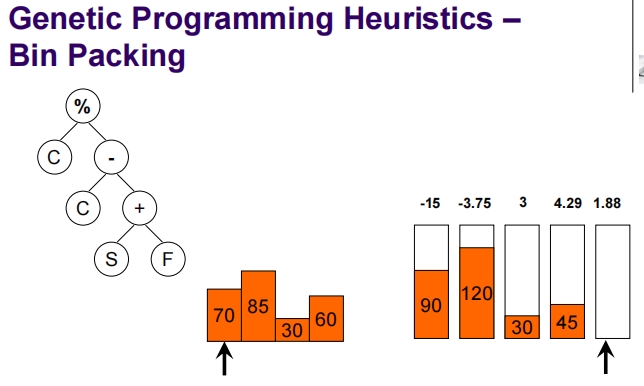
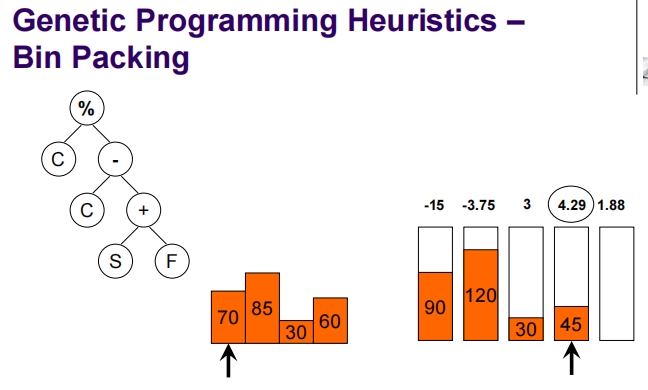
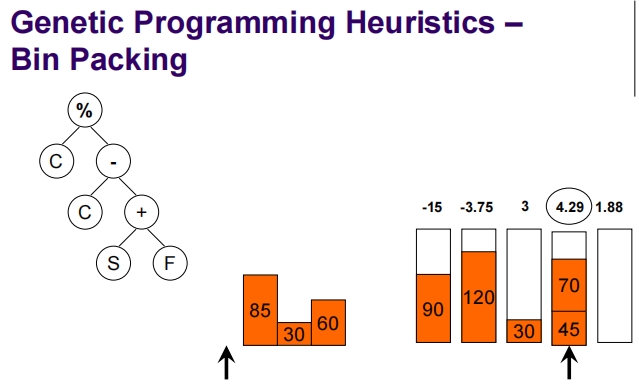
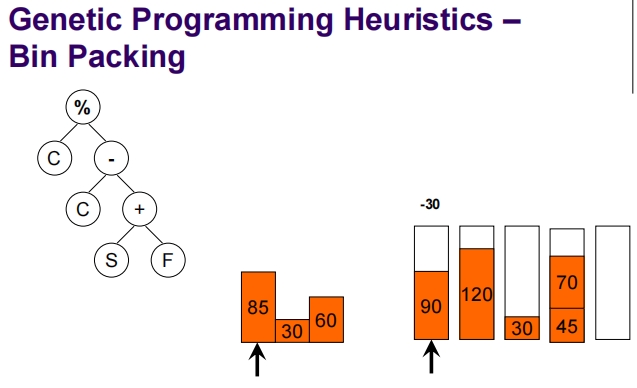
这张图片演示了遗传编程(GP)在1D在线装箱问题中的应用。通过GP生成的评分函数 ( f(r, s) ) 用于决定新物品应该放置在哪个箱子中。让我们来详细解析这个图中的信息:
图中展示内容
箱子情况:
- 四个箱子的剩余容量分别为:箱子0剩余2,箱子1剩余5,箱子2剩余4,箱子3剩余8。
- 新物品的大小为3。
评分计算:
- ( f(5,3) ):箱子0的评分为-1。
- ( f(4,3) ):箱子1的评分为1。
- ( f(8,3) ):箱子2的评分为-7。
- ( f(12,3) ):箱子3的评分为-15。
评分函数结构(( f(r, s) )):
- 函数表达式在图中通过一个算术函数树表示,树的根是加法节点,其子节点包括常数、箱子容量 ( C )、物品大小 ( s ) 以及剩余空间 ( r )。
解释和分析
- 在这个例子中,每个箱子的评分是根据 ( f(r, s) ) 计算得到的,该函数通过遗传编程自动设计。
- 新物品会被放入评分最高的箱子中。在这个场景中,箱子1的评分最高,因此新物品应该被放置在箱子1中。
- 通过遗传编程生成的评分函数允许系统以一种优化和动态调整的方式进行决策,适应不同物品和箱子状态的变化。
应用价值
遗传编程在在线装箱问题中的应用表明,可以通过自动化学习和适应过程,生成复杂但有效的评分函数。这种方法不仅减少了人为设计启发式的需求,而且提供了一种能够动态适应不断变化条件的智能系统。通过这种方式,系统能够更有效地管理资源,提高操作的效率和效果。

这张图片探讨了在使用遗传编程(GP)生成启发式评分函数时遇到的一些挑战。让我们逐一了解这些挑战:
挑战概述
函数空间难以理解:
- 在遗传编程中使用的函数空间可能很复杂,这使得理解和解释自动生成的函数变得困难。对于非专家用户来说,复杂的函数结构可能缺乏直观性和可解释性。
表示选择的偏见:
- 函数的表示方式(例如算术函数树)可能会引入偏见。选择不同的表示方法可能会导致搜索过程中的探索偏向特定类型的解决方案,而不是最优解。
“臃肿”的函数表示:
- 即使是性能良好的函数,也可能因为其在遗传编程中的表示过于复杂而被认为是“臃肿”的。这种臃肿不仅增加了计算负担,也可能掩盖了函数的实际效能。
改进的可能性
- 问题:“可以做得更好吗?”
- 对于这个问题,有几种可能的策略可以改进现有的方法:
- 简化表示:研究和开发更为简洁的函数表示方法,这可以帮助减少函数的复杂性和“臃肿”现象。
- 增强可解释性:引入机制以增强生成的函数的可解释性,比如通过可视化工具或将函数简化为更易于理解的形式。
- 优化算法本身:改进遗传编程的算法,例如通过引入新的遗传操作来减少偏见,或优化函数的适应性评估过程。
- 采用混合方法:结合遗传编程与其他机器学习技术,如强化学习或深度学习,来生成更为高效且实用的启发式函数。
总结来说,虽然遗传编程在自动生成启发式评分函数方面展示了巨大的潜力,但仍存在一些挑战,特别是在函数的复杂性和可解释性方面。通过研究和开发新的方法和技术,可以进一步优化这一过程,使其在实际应用中更为有效和用户友好。
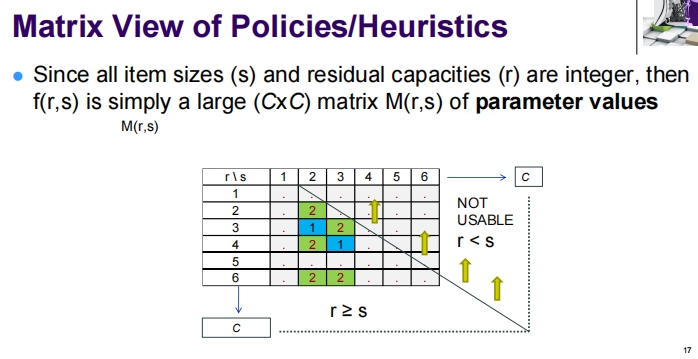
这张图片提供了一种将启发式评分函数 ( f(r, s) ) 用矩阵的形式表示的视角,适用于处理1D装箱问题中的物品大小和箱子剩余容量。这种表示法提供了一种直观的方法来查看和操作启发式策略。让我们详细解释图中的内容:
矩阵视图的解释
参数说明:
- s:物品大小。
- r:箱子的剩余容量。
- 这里的矩阵 ( M(r, s) ) 是一个 ( C \times C ) 的矩阵,其中 ( C ) 表示箱子的最大容量。
矩阵结构:
- 矩阵的行表示箱子的剩余容量 ( r ),从 1 到 ( C )。
- 矩阵的列表示物品的大小 ( s ),同样从 1 到 ( C )。
可用性标记:
- 当 ( r \geq s )(箱子的剩余容量大于或等于物品的大小)时,该格子被标记为可用,这意味着物品可以放入该箱子。
- 当 ( r < s )(箱子的剩余容量小于物品的大小)时,该格子被标记为“不可用”。
数值填充:
- 矩阵中的数值可能代表特定策略下的决策权重或优先级,比如在示例中,数字 1 和 2 可能表示不同的评分或策略决定。
应用价值和优势
- 简化决策过程:通过查看矩阵,可以快速识别哪些箱子能容纳新来的物品,以及放置物品的最佳位置。
- 直观操作:矩阵提供了一种直观的方式来调整和优化启发式策略,通过改变矩阵中的值,可以直接影响策略的行为。
- 方便扩展:这种方法可以轻易地扩展到更复杂或不同规模的问题,只需调整矩阵的大小和填充的值。
这种矩阵视图可以作为开发和测试新启发式策略的有力工具,使决策过程更加透明和可管理。此外,这种表示法也有助于在设计系统和算法时理解各种决策因素之间的相互作用。

这张图片展示了1D在线装箱问题中使用策略矩阵(Policy Matrix)的实例。图中结合了箱子当前状态和策略矩阵,来决定如何分配一个新到达的物品。下面是对图中各部分的详细解释:
图中展示的内容
箱子和物品状态:
- 四个箱子中物品的当前占用情况显示:箱子0剩有2单位,箱子1剩有5单位,箱子2剩有4单位,箱子3剩有8单位。
- 新到达的物品大小为3单位。
评分计算(( M(r, s) )):
- 箱子0(剩余容量2)对于大小为3的物品的评分是5。
- 箱子1(剩余容量5)的评分是7。
- 箱子2(剩余容量4)的评分是1。
- 箱子3(剩余容量8)的评分是3。
策略矩阵:
- 矩阵右侧显示,其中行表示箱子的剩余容量 ( r ),列表示物品的大小 ( s )。
- 矩阵中的星号(*)可能表示对于该 ( r ) 和 ( s ) 组合无效或不适用的情况。
- 具体数值(例如“5”,“7”等)表示对于给定的 ( r ) 和 ( s ) 组合,应用特定的评分策略。
决策:
- 根据评分,箱子1的评分最高(7),因此新物品将被放置在箱子1中。
解释和分析
- 图中的策略矩阵直观地展示了如何根据箱子的剩余容量和物品的大小来做出放置决策。
- 每个 ( (r, s) ) 组合的评分决定了新物品的放置位置。这种方法有助于优化空间利用,通过最大化特定评分标准(可能是空间利用率、成本效益等)来选择最佳的箱子。
- 策略矩阵使得决策过程更加标准化和自动化,减少了需要进行复杂计算的情况。
应用价值
这种矩阵视图为实时决策提供了一个清晰的框架,适用于需要快速响应的在线装箱环境,如仓库物流和货运包装。通过这种方式,可以系统地处理新物品的到来,优化整体装箱策略,提高效率和资源利用。

这张图片描述了在研究基于矩阵策略的均匀(随机)装箱问题实例的背景和设置。这里提供了生成这类问题实例的一种方法,被称为均匀装箱问题生成器(Uniform Bin Packing Problem Generator, UBP)。以下是其主要内容和参数:
主要内容和参数解释
问题生成器(UBP(C, (S_{\text{min}}), (S_{\text{max}}), N)):
- C:箱子的容量。
- (S_{\text{min}}):物品大小的最小值。
- (S_{\text{max}}):物品大小的最大值。
- N:生成的物品总数,通常很大,如100,000(100k),以模拟大规模的实际应用场景。
物品大小生成:
- 物品的大小是从 ([S_{\text{min}}, S_{\text{max}}]) 的范围内独立均匀随机抽取的整数。这意味着每个大小在指定范围内具有相同的出现概率。
应用价值和研究重点
- 实证研究:通过使用这种生成器,研究者可以在控制条件下测试和比较不同的矩阵策略在处理随机生成的均匀装箱问题实例时的效率和效果。
- 矩阵策略的优化:这种方法允许研究者观察不同物品大小和数量对矩阵策略性能的影响,从而优化这些策略以更好地应对各种场景。
结论
通过生成大量随机的装箱问题实例,可以广泛测试和验证装箱策略的稳健性和适应性。这种方法是理解和改进装箱算法在实际操作中表现的关键工具,尤其适用于物流、仓储和运输等领域,其中装箱效率直接影响到成本和时间效率。

这张图片描述了特定的装箱问题(Uniform Bin Packing, UBP)的设置和策略,特别是针对箱子容量为6,物品大小仅为2或3的情况。
问题设置
- **UBP(6, 2, 3)**:指的是箱子的容量为6,物品大小只有两种,即大小为2和大小为3。
- 完美的装箱方式:
- 2+2+2:使用三个大小为2的物品完全填满箱子。
- 3+3:使用两个大小为3的物品完全填满箱子。
推导的策略
- 基本策略:基于物品大小创建一个明显的规则,“从不混合偶数和奇数大小”,意味着不应将大小为2的物品(偶数)和大小为3的物品(奇数)放在同一个箱子中,以避免空间浪费。
矩阵策略解释
- 策略矩阵:
- 行(rows):表示箱子的剩余容量。
- 列(columns):表示物品的大小。
- 矩阵内容:显示在特定剩余容量下放入某大小物品的结果。例如,剩余容量为3的箱子放入大小为2的物品后剩余容量为1(显示为“1”),这是非理想状态,因为再也不能放入任何物品。
- 矩阵中的灰色条目:“.” 表示在该剩余容量下无法使用该大小物品,或该选择在策略上不可接受。
解决策略和实际应用
- 平局处理:如果两种选择都可用,使用首次适应(First-Fit, FF)策略来决定放置。
- 这种策略矩阵有助于快速决定每个新到达物品的放置,确保空间被最优化利用,避免因混合不合适大小的物品导致的空间浪费。
总结
这种策略矩阵为特定的装箱问题提供了一种清晰的视觉工具,有助于实现高效的装箱操作。它使操作者能够快速判断在给定剩余空间下哪些物品可以放置,以及如何放置以最大化箱子的利用率。这种方法特别适合需要处理大量相似规模问题的场景,如仓库物流、运输包装等。

这张图片介绍了一种名为 CHAMP(Creating Heuristics via Many Parameters)的方法,旨在通过使用大量参数来创建启发式策略。这种方法侧重于利用参数化的矩阵来调整和改善启发式函数,特别是在解决装箱问题时。下面详细解释这种方法的基本思想、预期效果以及潜在的缺点:
基本思想
- 参数化矩阵:将启发式函数 ( M(r, s) ) 中的值设定为整数,这些值可以通过元启发式搜索(如遗传算法、模拟退火等)来优化,以找到最佳的参数化决策。
- 模拟评估:通过模拟来评估不同的矩阵配置,以确定哪些配置最能有效地解决特定的装箱问题。
原始预期
- 性能提升:期望通过微调遗传编程(GP)生成的函数来改进性能,或者至少在一定程度上对其进行优化。
潜在的缺点
- 冗长性:与函数相比,矩阵可能更加冗长,因为它们包含了更多的参数。这可能导致处理和理解上的复杂性增加。
- 结构性缺失:矩阵可能没有函数那样能够很好地捕捉到某些有益的结构(例如函数的组合逻辑),从而可能忽略了一些有价值的决策规则。
分析与应用
CHAMP方法提供了一种新的途径来探索和优化装箱策略,特别是在那些参数空间庞大且问题结构复杂的场景中。通过细化参数和运用先进的搜索算法,这种方法能够在传统方法难以触及的领域内找到新的、可能更高效的解决方案。然而,随之而来的挑战是如何管理这些参数的复杂性以及如何确保解决方案的可维护性和可解释性。
总之,CHAMP尝试通过一个高度可定制化的框架来提高启发式的性能,虽然这可能会带来更高的计算成本和复杂性,但也为解决复杂的优化问题提供了潜在的新途径。
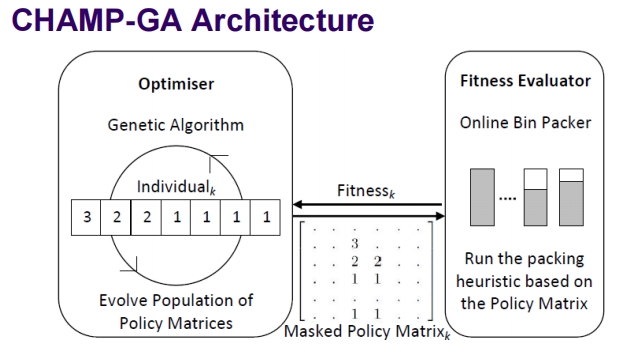
这张图片详细展示了CHAMP-GA(Creating Heuristics via Many Parameters using Genetic Algorithms)架构,一种结合了遗传算法和启发式策略矩阵的系统设计,用于优化在线装箱问题的解决方案。下面是对该架构的详细解释:
CHAMP-GA 架构组成
优化器(Optimiser):
- 使用遗传算法作为主要的优化技术,这是一种受自然选择启发的算法,用于在问题空间中搜索最优解。
- 遗传算法通过迭代过程中的选择、交叉(杂交)和突变操作来进化候选解,这里的候选解即为“个体”。
个体(Individual):
- 在CHAMP-GA中,每个个体代表一个策略矩阵,这些矩阵包含了决定如何放置物品的具体参数。
- 这些矩阵中的每个元素代表在给定的剩余容量和物品大小情况下的决策权重或规则。
蒙版策略矩阵(Masked Policy Matrix):
- 这是被选中用于当前迭代的策略矩阵,其可能经过了一定的修改和优化,以适应特定的装箱情况。
- 图中的矩阵展示了各种情况下的决策参数,如何在特定的容量和物品大小下做出最优决策。
适应度评估器(Fitness Evaluator):
- 该组件负责评估每个策略矩阵的效果,通过模拟在线装箱过程来测定其性能。
- 性能评价基于策略矩阵驱动的装箱效率,如何根据矩阵指示将物品放入箱子中,并计算所需箱子的数量和空间利用率。
性能和效果
- 适应度函数 ( Fitness_k ):用于测量给定策略矩阵在实际装箱任务中的表现,优化目标通常是最小化所需的箱子数量或最大化空间的利用率。
- 进化种群:随着算法迭代,种群中的策略矩阵将根据其适应度不断进化,淘汰表现不佳的矩阵,保留并通过交叉和突变产生更优秀的矩阵。
应用价值
CHAMP-GA架构提供了一种系统化方法来发展和细化装箱问题的解决策略。这种方法利用遗传算法的全局搜索能力,结合了策略矩阵的具体决策指导,能够逐渐找到更高效的装箱方法,适用于复杂的实际应用场景,如物流、仓库管理等领域。

这张图片提供了CHAMP-GA系统实现细节的详细信息,阐述了遗传算法(GA)在训练过程中的具体应用。以下是对这些实现细节的详细解释:
实现细节概述
标准遗传算法应用:
- 跨代遗传:使用弱精英主义策略,确保部分优秀个体能够被保留到下一代。
- 种群大小:设为 ( C/2 ),其中 ( C ) 为问题的上下文参数,可能代表总箱子数或其他相关参数。
- 锦标赛选择:每次选出两个个体(tour size: 2),比较其适应度,选择较好者进行交叉或变异。
- 均匀交叉:父母染色体均等地贡献基因给后代。
- 标准变异:以 ( 1/L ) 的概率进行,其中 ( L ) 可能代表染色体长度。
- 迭代次数:算法在200次迭代后终止。
染色体存储:
- 只有矩阵的活跃成员(有效的决策参数)被存储为整数或二进制值。
- 初始种群中的染色体(GA_Finit)由代表首次适应策略(FF)的个体开始,这提供了一个基线策略的基因起点。
评估机制:
- 将策略矩阵写入文件,这可能用于记录、分析或进一步处理。
- 使用这些矩阵作为输入,运行一个程序来模拟多个物品的装箱过程,以此评估矩阵的有效性和效率。
图中图示
- 图中的图表显示了随着迭代次数的增加,某个度量(可能是适应度、错误率或其他性能指标)如何变化,显示出随着时间的推移性能有所改善。
结论
这种详细的实现说明确保了遗传算法能够高效地用于优化装箱问题的启发式策略矩阵。通过精确控制遗传操作和适应度评估,CHAMP-GA可以系统地改进装箱策略,使之更加适应各种装箱挑战。此外,初始种群的设置和评估方法的选择都是为了确保算法从一个合理的基线开始,逐步探索出更优解。这种方法展示了高度专门化的遗传算法如何应用于复杂的实际问题中,提供了一个强大的工具来改进和优化决策过程。
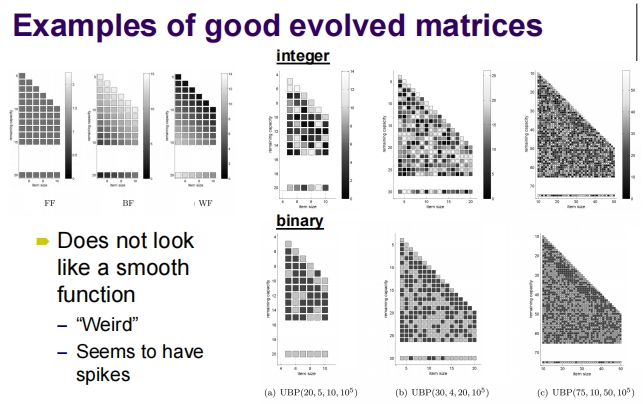
这张图片展示了一些通过遗传算法优化得到的策略矩阵,用于解决不同配置的均匀装箱问题(UBP)。这些矩阵是在CHAMP-GA框架下进化而来,显示了整数和二进制两种形式的矩阵。以下是对图中内容的详细解析:
图中展示的矩阵
- 左侧三个矩阵:展示了基于传统启发式策略如首次适应(FF)、最佳适应(BF)、最差适应(WF)生成的矩阵。
- 右侧六个矩阵:
- 分为上下两行,上行为整数形式的矩阵,下行为二进制形式的矩阵。
- 这些矩阵对应不同的UBP问题实例设置,如
(20, 5, 10, 10^5)表示箱子容量为20,物品大小在5到10之间,总共有100,000个物品。
特点和观察
矩阵形态:
- 这些矩阵呈现出不规则的模式,不像典型的平滑函数。其中的黑色和灰色块表示了不同的决策权重或规则。
- 图中指出,这些矩阵看起来“奇怪”,并且似乎有很多突出的峰值(spikes),这可能是遗传算法在适应特定问题约束时的结果。
整数 vs. 二进制矩阵:
- 整数矩阵可能提供了更详细的决策参数,而二进制矩阵则以更简化的方式表示决策,仅指示是否适合采取某种行动。
应用和解释
- 这些矩阵的复杂和非典型模式反映了装箱策略在特定约束下的优化。虽然它们看起来不像平滑或常规的函数,这种“非典型”外观可能代表了对特定问题环境下装箱效率的深度适应。
- 优化后的矩阵能够更精准地反映如何在实际操作中处理装箱,例如,在特定剩余空间和物品大小下最优地分配物品。
- 这些矩阵可以直接应用于在线或离线装箱算法中,提供基于经验和数据驱动的决策支持。
总结
展示的这些矩阵是遗传算法在解决具有复杂约束的优化问题时的典型产物。它们通过实际的性能评估来调整和完善,为装箱问题提供了根据具体条件定制的解决方案。这种方法在物流、仓储管理和其他需要动态资源分配的领域尤其有价值。
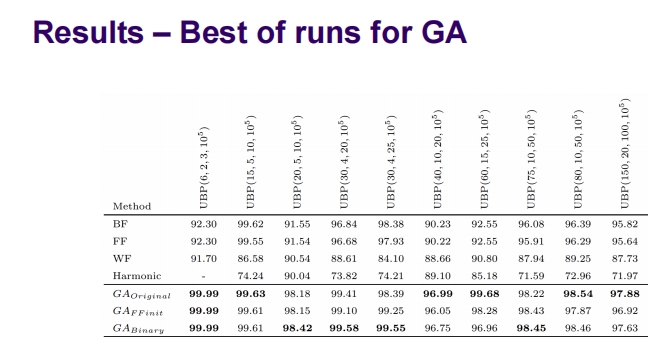

这张图片总结了使用标准元启发式方法生成表达为矩阵的策略的关键结论。以下是对这些结论的详细解析:
结论概览
使用标准元启发式生成策略:
- 证明了可以有效地使用如遗传算法这样的标准元启发式方法来创建优化的策略矩阵,这些矩阵以直观和可操作的形式表达决策策略。
性能超越传统启发式:
- 开发出的策略在某些情况下能够超过传统的启发式方法,如首次适应(FF)或最佳适应(BF)。
策略发现的便利性:
- 发现有效策略的过程比预期更容易,说明元启发式方法在这类问题上的应用具有高效性。
多样性和非常规性:
- 存在多种性能相近的策略,显示了解决方案的多样性。
- 这些策略往往比预期的更为“怪异”,具有难以通过常规代数函数(如遗传编程中使用的)捕捉的随机或复杂结构。
策略的可分析性:
- 尽管策略结构可能复杂或随机,但结果仍然可以分析(检查),以识别和提炼出性能优良的简单策略。
- 这些策略可扩展到更大规模的问题,显示了其可用性和扩展性。
应用和影响
- 策略开发的灵活性和适应性:元启发式方法通过提供一种能够适应各种问题约束的灵活方式,使得策略开发不受限于传统的算法或模型。
- 优化策略的实际应用:这些策略可以直接应用于实际的装箱问题,可能涉及物流、仓储管理等行业,其中效率的微小提升也可能带来显著的经济效益。
总结
这项研究表明,使用元启发式方法来发展和优化装箱策略是可行的,且常常能超越传统方法。通过这种方法,可以系统地生成、评估和优化决策矩阵,从而在复杂的装箱问题中找到更有效的解决方案。此外,这种方法的适应性和灵活性使其成为解决其他优化问题的有力工具。
Data Science (Machine Learning) Improved Hyper-heuristic Optimisation

这张图片介绍了一种名为“单目标超启发式”的数据科学改进方法。它侧重于如何利用多维数据,特别是在解决高维问题时的优化和效率提升。以下是对这种方法的详细解释:
主要内容
多维数据的挑战:
- 许多现实世界中的数据集都是多维的,常常具有很高的维度和大量的冗余信息。
- 这些数据需要复杂的处理方式来有效地提取有用信息,并优化存储和分析过程。
多维数组和张量:
- 描述这类数据的多维数组称为张量,它是向量和矩阵的高维推广。
- 张量能够更加全面地表示数据的多维关系,是理解和处理复杂数据结构的关键工具。
应用领域:
- 张量和多维数据分析方法在许多领域有广泛的应用,如信号处理、心理计量学、社会网络分析、基因组学等。
- 这些领域中的问题常常涉及到从大量多维数据中提取信息,分析时间序列,或者识别空间模式等。
改进的超启发式
- 这种方法使用数据科学技术来改进超启发式算法,使之能够更好地处理多维数据问题。
- 通过整合数据科学的方法和传统的优化技术,可以开发出更加精确和高效的算法,这些算法在处理具有高复杂度和大规模数据集的问题时表现优越。
结论和影响
- 该方法不仅提供了一个框架来解决高维优化问题,还能通过数据科学的视角来改进算法设计和实现,使其在实际应用中更加有效。
- 将这些技术应用于数据密集型领域,可以显著提高分析的准确性和决策过程的效率,对科学研究和工业应用都具有重要意义。
总之,通过整合数据科学和超启发式方法,可以创建出能够更好地理解和处理多维数据的高级算法,这为处理当今世界中越来越复杂的数据问题提供了新的工具和方法。

这张图片介绍了张量分解的一个具体例子——典型多项式(Canonical Polyadic, CP)分解,这是一种用于分析和简化多维数据的方法。以下是对图中内容的详细解释:
张量分解的基本概念
不同的分解方法:
- 张量分解有多种方法,其中CP分解是最常见的一种形式,用于将三维或更高维度的数据分解成较为简单的数学结构。
CP分解的定义:
- CP分解将一个张量 (\hat{T}) 表达为若干个秩为1的张量的和:
[
\hat{T} = \sum_{k=1}^K \lambda_k ; a_k \otimes b_k \otimes c_k
] - 其中 (\lambda_k) 是标量,(a_k), (b_k), (c_k) 分别是与每个模式(维度)相关的向量,(\otimes) 表示张量积。
- CP分解将一个张量 (\hat{T}) 表达为若干个秩为1的张量的和:
CP分解的应用和好处
数据投影:
- CP分解允许将三维数据投影到一维向量上,这有助于减少处理和分析数据时所需的计算量。
- 通过这种方式,可以更高效地处理和分析大规模的多维数据。
揭示潜在结构:
- CP分解有助于揭示数据中的潜在结构,通过量化不同组成部分之间的关系来提供深入的数据洞察。
- 这种分解方法特别适用于那些需要从复杂数据集中提取简洁信息的场景,如图像处理、信号处理等领域。
图中的示例
- 图中展示了一系列二维图像,这些图像可能代表了张量分解前后的一些状态。这些图像通过可视化来说明CP分解如何影响数据表示,具体体现了数据从复杂多维结构到简化表示的转变。
总结
CP分解是一种强大的多维数据分析工具,通过将复杂的数据结构分解为更简单的数学形式,它不仅能简化数据的处理和分析过程,还能帮助科研人员和工程师揭示和理解数据中隐藏的模式和结构。这种方法在数据科学、机器学习、网络分析等多个领域都有广泛的应用,是现代数据分析不可或缺的工具之一。

这张图片描述了一种平衡探索和利用的提议方法,主要在启发式搜索算法中使用,如迭代局部搜索(Iterated Local Search, ILS)。以下是对这种方法和提出的主要思想的详细解释:
提议方法的关键点
探索与利用的平衡:
- 在任何启发式搜索过程中,平衡探索(探索新解决方案)和利用(优化已知解决方案)是至关重要的。
- 图中的时间轴显示了在不同时间点上重点放在利用或探索上。这种交替策略有助于避免局部最优同时增加解决方案空间的覆盖范围。
启发式集合(( h )):
- ( h ) 表示用于搜索的低级启发式的集合,包括多种类型的启发式,如MU(可能是Mutation),RC(可能是Recombination),LS(Local Search)等。
- ( h_{IE} ) 和 ( h_{NA} ) 分别代表互斥的启发式子集,即 ( h_{IE} \cup h_{NA} = h ) 且 ( h_{IE} \cap h_{NA} = \emptyset )。
混合移动接受方法:
- 指的是在搜索过程中采用不同的策略来决定是否接受新的解决方案,例如,根据某种准则接受或拒绝对当前解决方案的修改。
应用机器学习:
- 使用机器学习技术来分区低级启发式,根据每种方法与特定启发式的关联性分配启发式。这可能涉及到分析哪些启发式在哪些情境下最有效,从而动态调整搜索策略。
应用场景和影响
- 这种方法特别适合于需要在探索新解决方案空间和精细调整已发现解决方案之间动态切换的复杂优化问题。
- 通过有效地切换探索和利用模式,可以在更广泛的解决方案空间内找到全局最优解,同时避免过早收敛于局部最优。
- 引入机器学习可以进一步优化这一过程,通过智能化分析历史数据和性能指标来自动调整和选择最合适的启发式方法。
总结
此提议方法不仅增强了启发式搜索的灵活性和有效性,还通过集成机器学习提高了其自适应能力。这种策略对于解决各种需要复杂决策和优化的实际问题尤其有价值,如物流优化、网络设计、生产调度等领域。通过不断学习和适应,该方法能够提供更精确、更高效的解决策略。
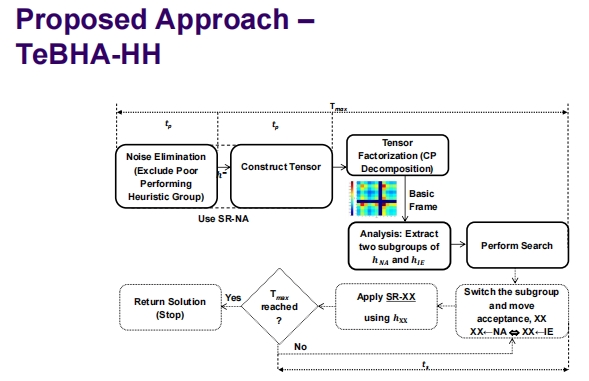
这张图片展示了一个名为 TeBHA-HH(Tensor-Based Hyper-Heuristic)的提议方法流程图,这是一个基于张量和数据科学技术的高级启发式搜索方法。这个方法特别关注于如何通过高级数据处理和优化技术来提升启发式算法的性能。以下是对该流程图的详细解析:
TeBHA-HH 方法流程
噪声消除:
- 这一步骤涉及去除性能较差的启发式群组。这可能是基于之前迭代中这些启发式的表现,从而确保算法集中资源在表现更好的启发式上。
构建张量:
- 利用收集到的数据(可能包括启发式的性能指标或其他相关信息)构建多维数据结构,即张量。
**张量分解 (CP Decomposition)**:
- 采用典型多项式分解来简化张量,这有助于识别数据中的关键模式和关系,从而更好地理解各启发式间的相互作用。
基本框架分析:
- 分析分解后的张量,提取两个子群组 ( h_{NA} ) 和 ( h_{IE} ),这可能是基于启发式的特定属性或它们在解决问题中的角色。
执行搜索:
- 使用提炼后的启发式信息执行搜索任务,优化问题的解决策略。
应用 SR-XX:
- 这可能指的是特定的搜索规则或方法,用 ( h_{XX} )(从张量分析中得到的启发式信息)来指导搜索。
切换子群组:
- 在确定的时间点或条件下切换使用的启发式子群组,并移动接受准则从 ( XX-NA ) 到 ( XX-IE ),可能是为了从广泛探索切换到更集中的利用。
终止条件:
- 当达到最大时间 ( T_{max} ) 或其他预设的停止条件时,返回解决方案并停止算法。
方法特点和优势
- 数据驱动:通过使用张量和高级数据分析技术,该方法可以在不同的启发式之间进行智能选择和切换,大大提升搜索的效率和效果。
- 动态适应:能够根据问题的具体情况动态调整使用的启发式,使算法能够自适应地应对不同的挑战。
- 全面分析:通过张量分解揭示的深层次数据关系为算法提供了强大的决策支持,使得算法不仅基于表面的性能指标,而是更深层次的数据洞察进行决策。
总结
TeBHA-HH方法提供了一种结合了先进的数据科学技术和传统启发式搜索的复杂但强大的算法框架。这种方法特别适用于解决那些需要处理大量数据和多变因素的复杂优化问题,如在工业、物流和金融等领域中常见的问题。
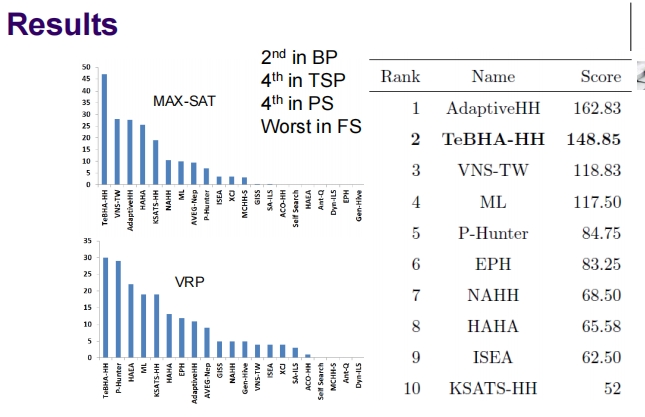
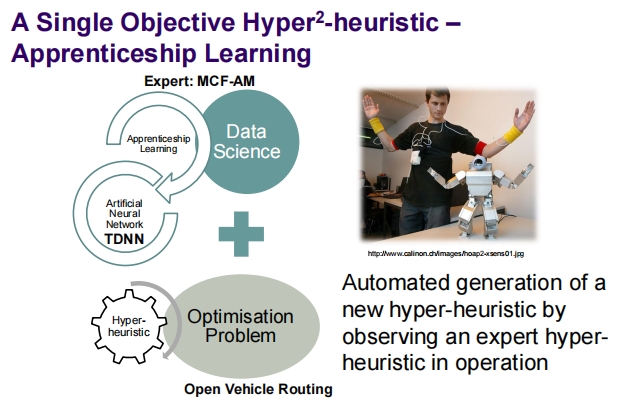
这张图片展示了一种基于学徒学习(Apprenticeship Learning)的单目标超启发式方法,其应用于优化问题,如开放式车辆路线问题。以下是对该方法的详细解析:
学徒学习的超启发式方法核心概念
学徒学习与数据科学的结合:
- 学徒学习:这是一种通过观察和学习专家的行为来自动创建新算法的方法。在这种情境下,专家是一个先进的超启发式算法(标记为 MCF-AM)。
- 数据科学:利用数据科学技术来分析和理解专家超启发式的决策过程,进而模拟这些策略。
人工神经网络TDNN:
- TDNN(Time-Delay Neural Network)通常用于处理序列数据或时间序列预测问题。在这里,它可能被用来模拟和预测优化过程中的决策模式。
超启发式与优化问题:
- 超启发式:一个高级的算法框架,用于从一组可能的启发式方法中选择最优的解决方案策略。
- 优化问题:具体的案例是开放式车辆路线问题,这是一个经典的物流和运输问题,涉及如何最有效地规划车辆路线以降低成本并提高效率。
方法的操作和优势
自动化生成新超启发式:
- 通过观察专家超启发式在实际操作中的表现,学习其策略和决策过程。
- 使用人工神经网络来模拟这些行为,并生成能够模仿专家决策的新超启发式。
解决具体的优化问题:
- 将学到的策略应用于具体的优化问题,如开放式车辆路线,验证新超启发式的有效性和效率。
- 这种方法的自动化和智能化水平高,可以减少人工干预,提高解决问题的速度和质量。
总结
通过将学徒学习和人工神经网络技术应用于超启发式方法,这种策略为处理复杂的优化问题提供了一种新的途径。它不仅能学习现有的优秀策略,还能在此基础上创新,生成适应新挑战的解决方案。这种方法的应用潜力巨大,特别是在需要高度自动化和智能决策支持的领域。


这张图片提供了关于超启发式研究的两部分总结,概述了该领域的关键发展、挑战和未来方向。
总结 I:超启发式研究的起源和发展
起源:
- 超启发式研究起源于作业车间调度应用,此后迅速发展扩展至其他领域。
生成超启发式的常用方法:
- 在训练和测试模式下普遍使用,涉及选择一个代表性的训练实例子集来训练算法,再用测试集评估其性能。
- 训练过程可能耗时且复杂,涉及增量评估和替代函数的使用。
生成/进化启发式的特点:
- 虽然这些启发式可能不易解释,但它们能够超越人类设计的启发式,显示出卓越的性能。
总结 II:机器学习/数据科学在超启发式中的应用及挑战
机器学习/数据科学的应用证据:
- 有实证数据显示,机器学习和数据科学技术能显著改善超启发式搜索过程。
- 应用包括分析问题特征与解决方案/状态特征,支持离线与在线学习,及其对终身学习的贡献。
存在的挑战:
- 尽管取得了进展,但超启发式研究仍面临基准测试不足的问题,这限制了方法间比较的客观性和广泛性。
- 搜索方法论的自动设计极具挑战性,特别是在缺乏数学和理论上的深入理解的情况下。
影响与未来方向
- 这些总结指出,超启发式领域在理论和应用层面都有广阔的发展前景。尤其是将数据科学和机器学习技术引入超启发式设计,为解决复杂的优化问题提供了新的思路和方法。
- 未来的研究可能会更多地集中在提高算法的解释性,发展更为系统的基准测试,以及探索更有效的自动化设计方法来应对实际应用中的挑战。
这些总结为超启发式研究和应用提供了重要的洞见,特别是在如何利用现代技术来推动该领域前进的方面。