记得这是初中非常喜欢的一首歌，那时还在用QQ音乐，希望大家下面的知识“All We Know”😋

Lecture01

Primitive Operations

两种计数方式

Count Operations (by second way)

Exercise

Method1(常规算数)

Method2(二进制位移)

计算循环次数

Answer

Lecture02

Big-Oh 表示法是用于描述算法复杂度的一种方式，特别是在计算机科学中用来表征算法的运行时间或所需空间与输入大小之间的关系。Big-Oh 是“渐进上界”的缩写，它提供了一个算法可能的最慢运行速度的上限。重要的是要注意，Big-Oh 并不试图精确描述算法在特定情况下的表现，而是试图提供一个随着输入规模增加时，算法表现的大致趋势。

Big-Oh 表示法的基本概念

• 定义：如果存在正常数 (C) 和 (n_0)，使得所有 (n >= n_0) 时，(f(n)<= C * g(n))，则我们可以说 (f(n)) 在渐进意义上小于等于 (g(n))，记为 (f(n) = O(g(n)))。
• 直观含义：这意味着当输入规模足够大时，算法的运行时间（或空间需求）不会超过 (g(n)) 的某个常数倍。(g(n)) 提供了一个“上限”。
• 常见的Big-Oh 类别：
  • 常数时间：(O(1)) 表示算法的运行时间不随输入规模的增加而改变。
  • 线性时间：(O(n)) 表示算法的运行时间与输入规模成正比。
  • 二次时间：(O(n^2)) 表示算法的运行时间与输入规模的平方成正比。
  • 对数时间：(O(\log n)) 表示算法的运行时间与输入规模的对数成正比。
  • 线性对数时间：(O(n\log n)) 常见于某些高效的排序算法中。
  • 指数时间：(O(2^n)) 表示算法的运行时间随输入规模的增加而呈指数级增长。

Big-Oh 表示法的使用

Big-Oh 表示法在分析算法时非常有用，它帮助我们理解算法在处理大量数据时可能遇到的性能瓶颈。通过比较不同算法的Big-Oh 复杂度，我们可以预测哪种算法在面对大规模输入时更加高效。

重要性

• 性能预测：帮助预测算法在处理大规模数据集时的行为。
• 算法比较：提供了一种标准化的方法来比较不同算法的效率。
• 性能优化：指导开发人员识别并优化代码中的性能瓶颈。

总之，Big-Oh 表示法是理解和比较算法性能的关键工具，它强调了算法性能随输入规模变化的趋势，而不是具体的运行时间。

不等式含义

在不等式 (f(n)<= c * g(n)) 中，用于描述Big-Oh 表示法的关系时：

• (f(n)) 代表算法的实际运行时间或所需资源（如操作的次数）作为输入大小 (n) 的函数。
• (g(n)) 是一个简化的函数，用来表示 (f(n)) 的增长率上界。
• (c) 是一个正常数，用于确保 (f(n)) 的值不超过 (c*g(n))。

在这个上下文中，(f(n)) 通常代表算法在最坏情况下的性能。这意味着，对于所有可能的输入 (n)，算法的性能（或复杂度）不会比 (c*g(n)) 更差。换句话说，(g(n))（经过适当的常数 (c) 缩放）提供了算法最坏情况性能的一个上界。

因此，最坏情况是通过 (f(n)) 来表示的，而 (g(n)) 是用来量化或界定这个最坏情况性能的增长速度的函数。Big-Oh 表示法 (O(g(n))) 用来说明无论算法面临怎样的输入，其性能的增长速度都不会超过函数 (g(n)) 的某个常数倍。

Big Oh as a binary relation

Big-Oh is Reflexive

Big-Oh is not symmetric

Big-Oh is transitive

Big-Oh as a set

Lecture03

“Multiplication Rule” for big-Oh

Big-Oh Rules: Drop smaller terms（构造出会趋近于0的部分）

Big-Oh Rules

Seven Important Functions

Recall: “Drop smaller terms”

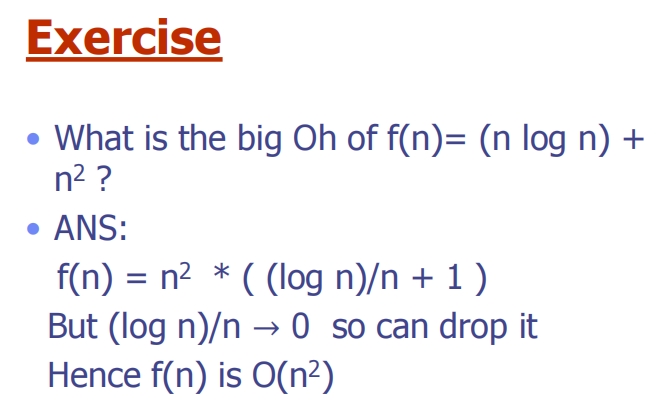
Big-Oh Conventions

Lecture04

Big-Omega

Big-Theta

这意味着在最坏情况和最佳情况下，算法的时间复杂度都是相同的阶。

Big-Theta is reflexive , transitive and symmetric

Θ is an equivalence relation

Little-Oh

这通常用于表明某个算法的性能比另一种具体增长率要好，但并不达到那个界限

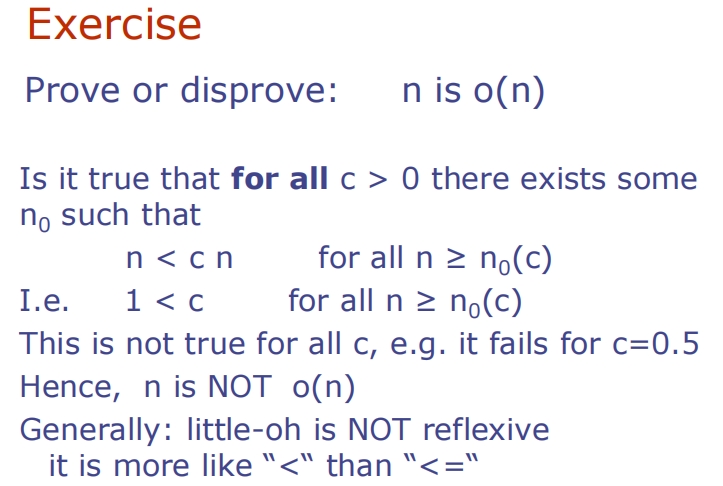
Intuition or ‘mnemonics’ for Asymptotic Notation

考试证明

Big-O证明

$O(n)$​证明

或者

1. choosing $c=3$ gives $1 \leq (3-2)n, \forall n \geq n_0$ （选择c的值，写出式子和n范围）
2. which simplifies to $1 \leq n, \forall n \geq n_0$ （简化式子得到n的范围）
3. From this we can see that $n_0 \geq 1$ （给$n_0$取范围）
4. which gives $1 \leq n, \forall n \geq 1$​ which is trivially true (得到n的取值范围，然后所有在这个范围的n都能成立)
5. $\therefore 2n+1 \text{ is } O(n)$​ using $c=3$​ and $n_0 = 1$​. （告诉他这个属于O(?)，当$c=?, n_0$​​​=?）

Disprove Big-O

Drop Smaller证明

Lecture05

“Multiplication Rule” for big-Oh * little-Oh

Lecture06

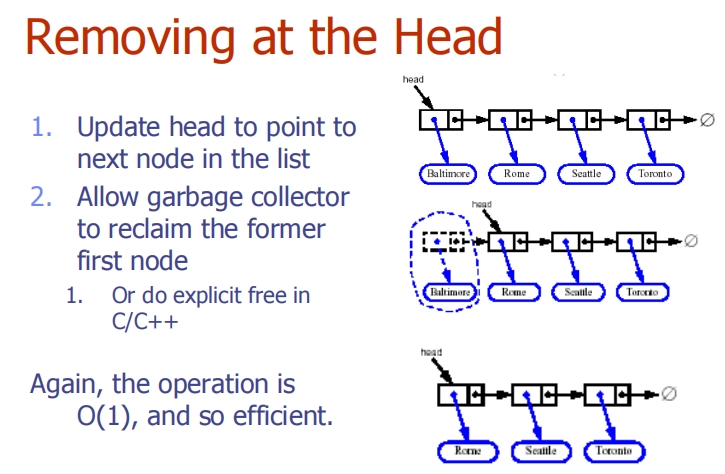
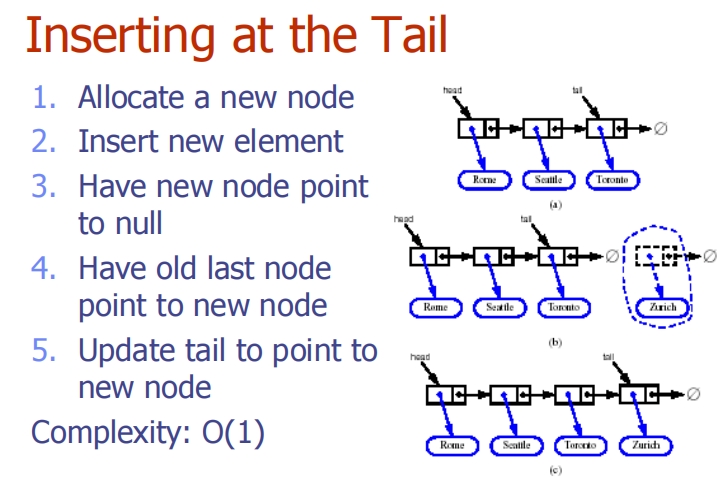
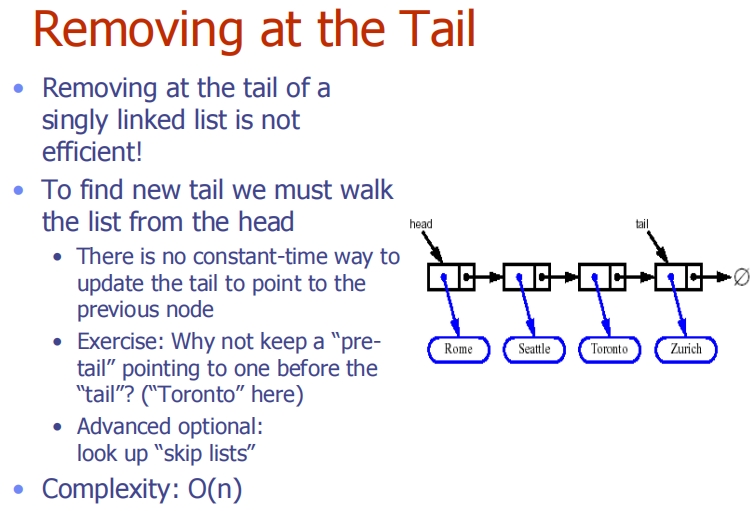
Singly Linked List

Doubly Linked List

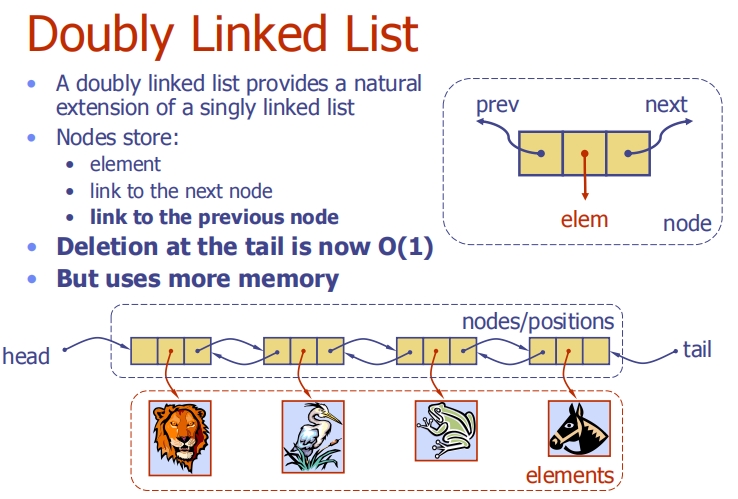
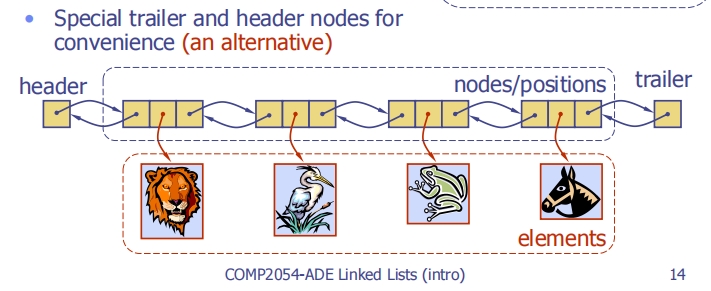
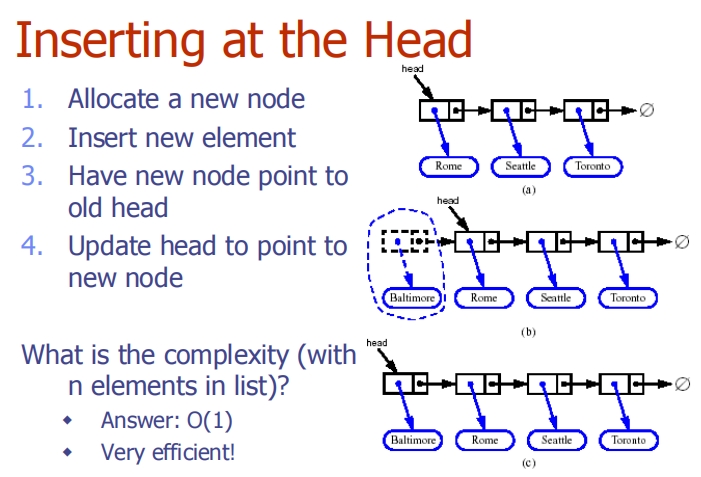
Insertion

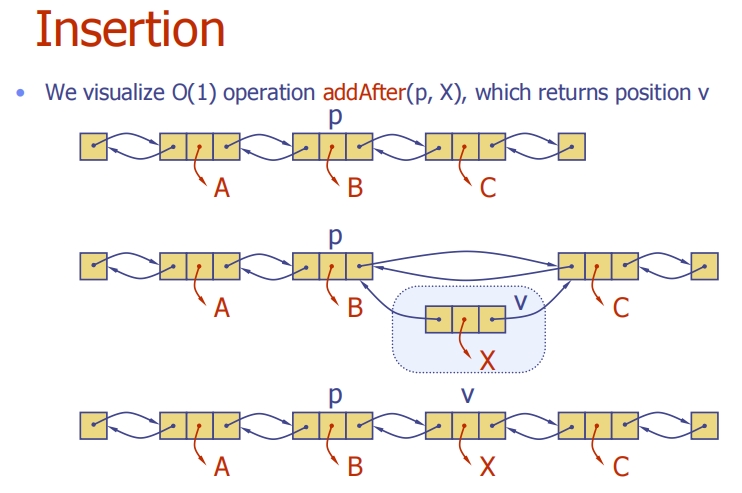
Insertion Algorithm

Lecture07 (Simple Sorting Algorithms)

Bubble Sort ( O(n^2) ）

比较相邻元素，如果前一个比后一个大，就交换他们两个。对每一对相邻元素做同样工作，从开始第一队到结尾最后一对。针对所有的元素重复以上的步骡直到没有任何一对数字需要比较。

Complexity of bubble sort

Complexity of bubble sort on lists

Selection Sort ( O(n^2) ）

首先在未排序序列中找到最小(大)元素存放到排序序列的起始位置，再从剩余未排序元素中继续寻找最小(大)元素然后放到已排序序列的未尾，重复上一步直到所有元素均排序完毕

Complexity of selection sort

Selection sort on linked lists

Insertion Sort 时间复杂度( O(n^2) ）空间复杂度( O(1) ）

将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列，从头到尾依次扫描未排序序列将扫描到的每个元素插入有序序列的适当位置

Complexity of insertion sort

Insertion sort on linked lists

Lecture08 (Trees)

Traversals

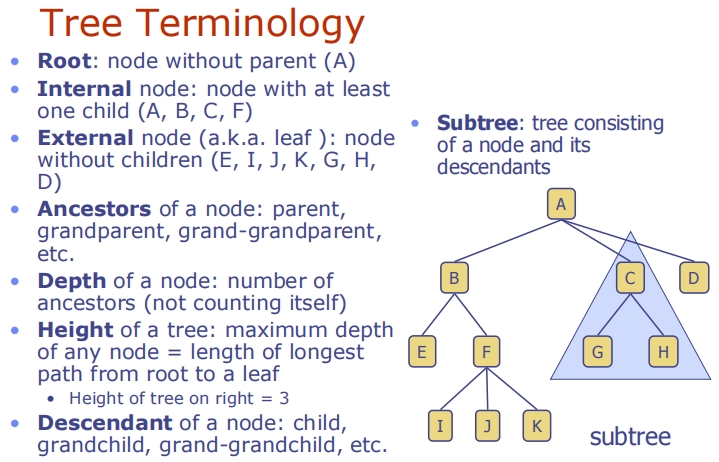
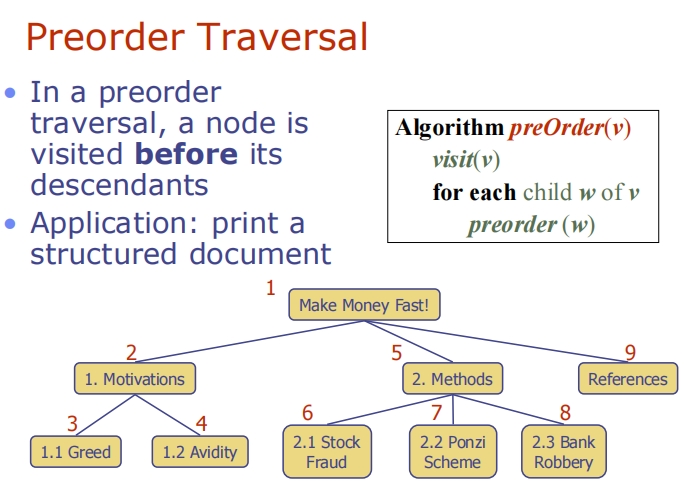
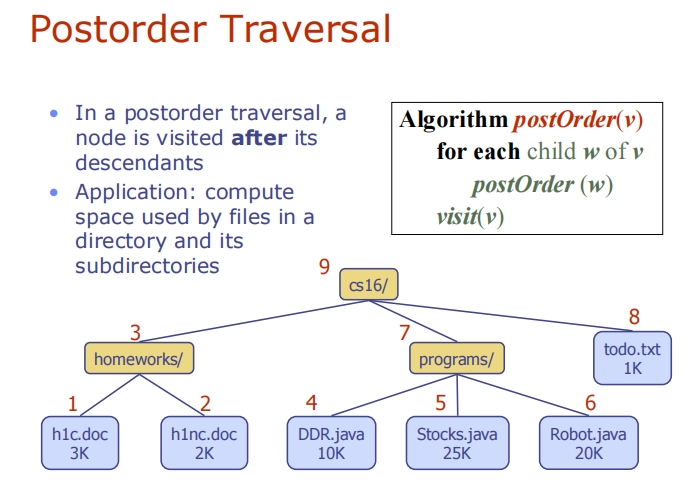
Binary Trees

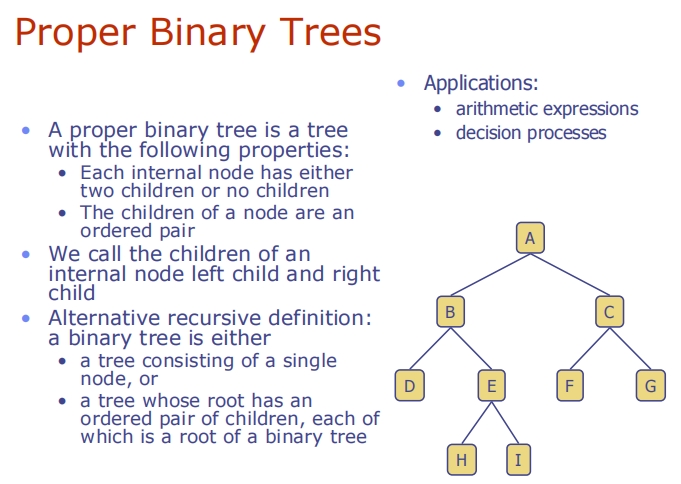
Arithmetic Expression Tree

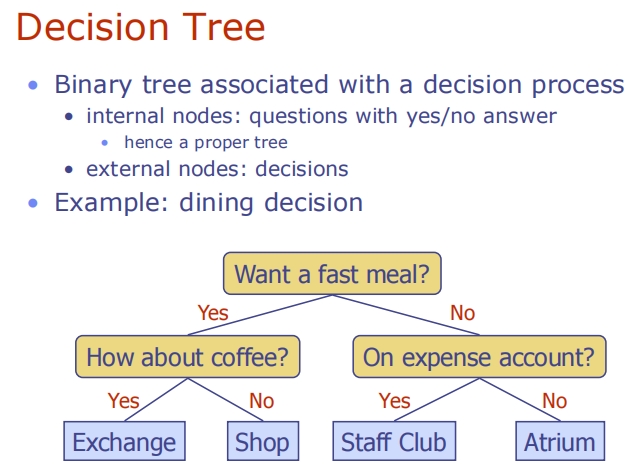
Decision Tree

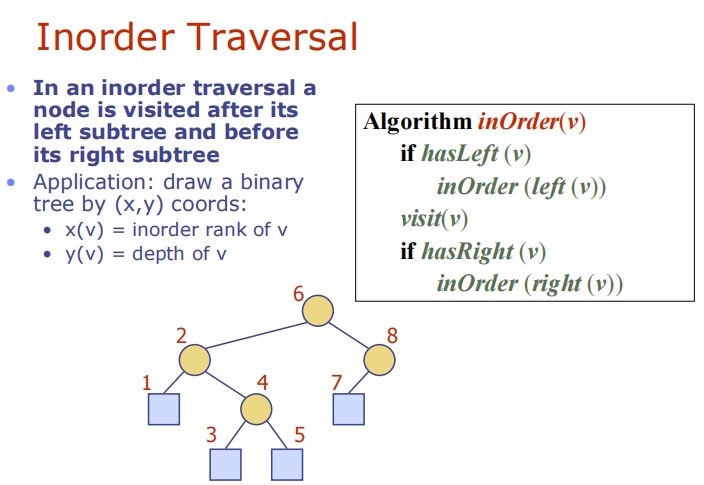
Inorder Traversal

Print and Evaluate Arithmetic Expressions

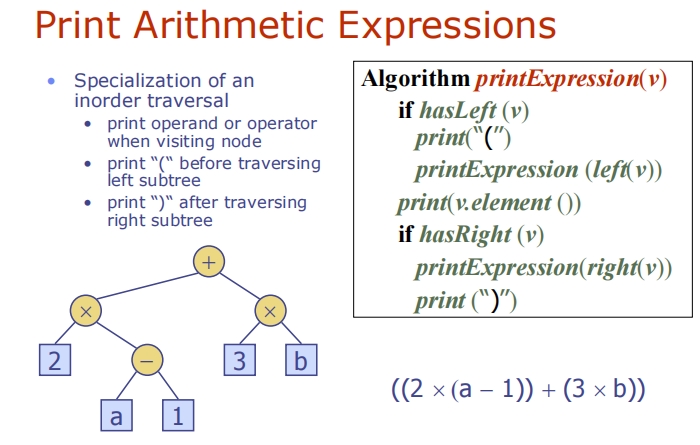
Linked Structure for Trees

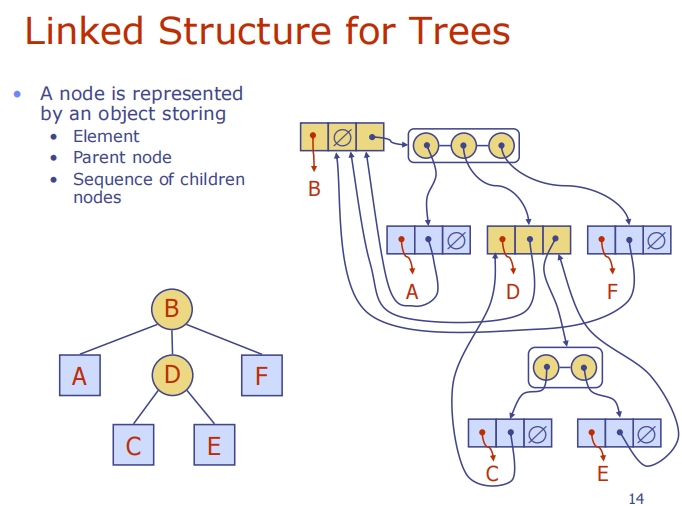
Linked Structure for Binary Trees

Abstract Data Types (ADTs) and Concrete Data Types (CDTs)

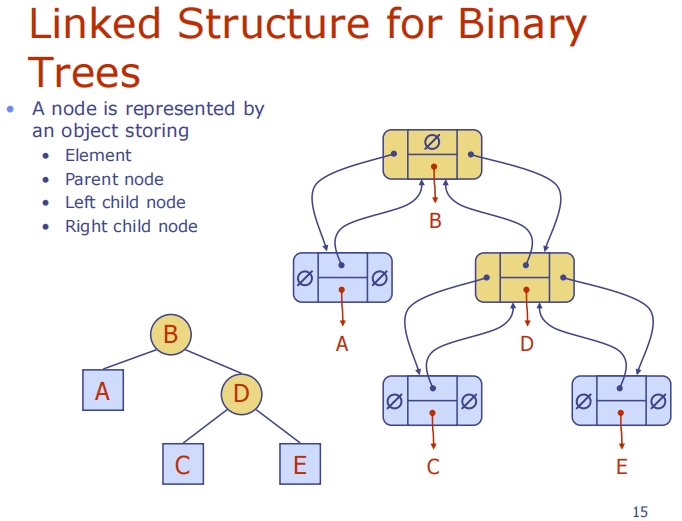
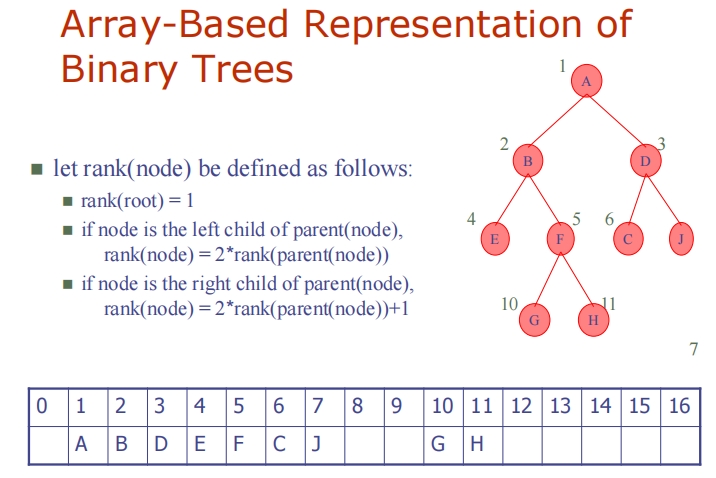
Array-Based Representation of Binary Trees

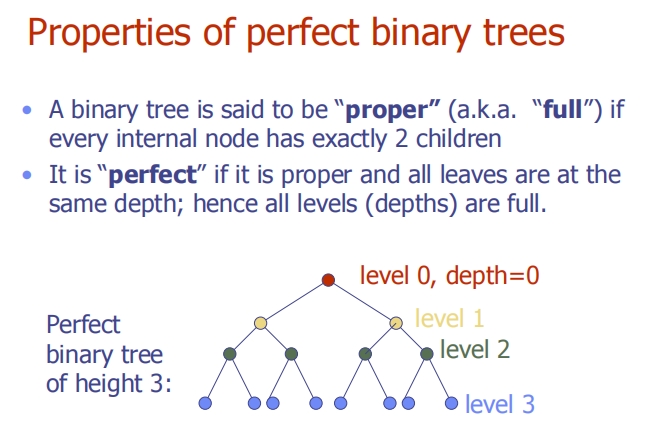
Properties of perfect binary trees

Lecture09 (Mergesort)

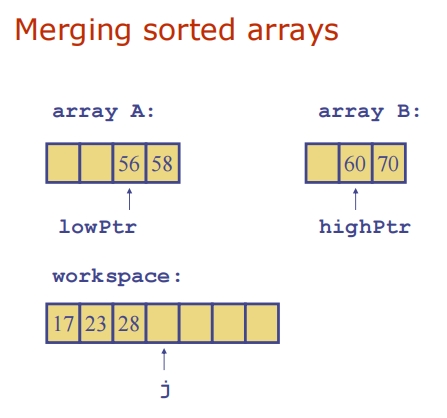
Merge-Sort Tree

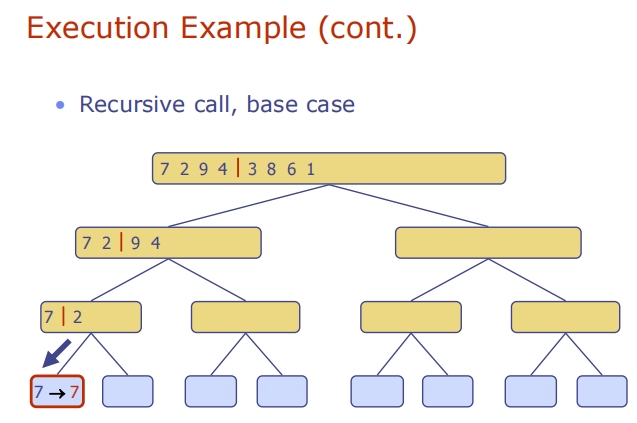
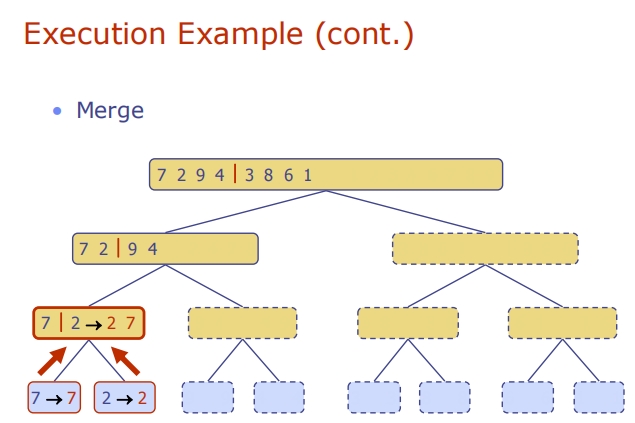
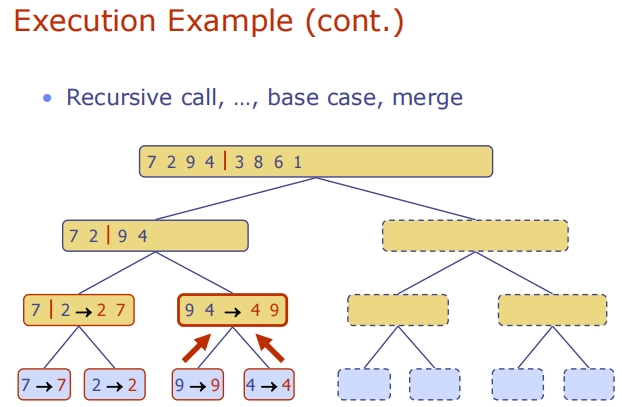
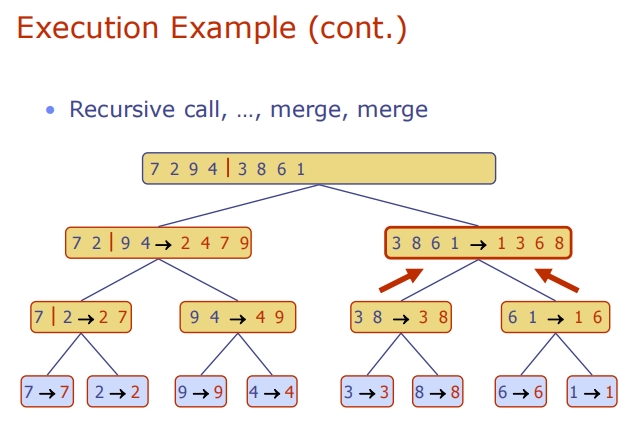
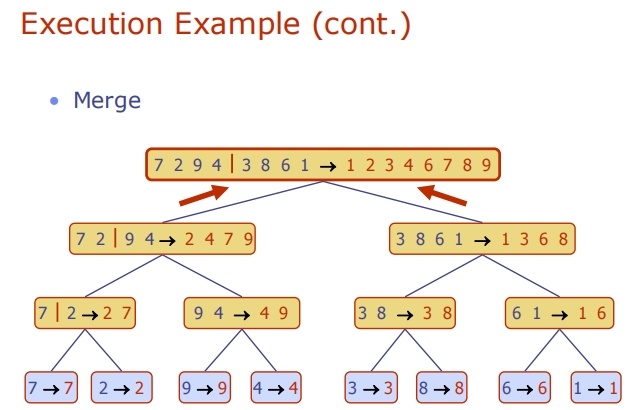
Lecture10 (Recurrence Relations递归关系)

Example1

Example2

Example03

Example4

Example5

Example6

Simple sorting?

Example7

Lecture11 (The “Master Theorem”)

Master Theorem (MT): Cases

MT: Case 1

MT: Case 2

MT: Case 3 (还要证明满足Regularity Condition)

Regularity Condition (case 3)

Lecture14 (The Vector Data Type, and Amortised Analysis)

这张幻灯片介绍了“向量”（Vector）这一抽象数据类型（ADT）。向量是对数组概念的一种泛化，其中的“数组”是具体的数据类型（CDT）。幻灯片的核心思想是，数组中某个元素的索引可以被视为在它之前的元素数量，即在数组 A 中，A[2] 前面有两个元素 A[0] 和 A[1]。在这些讲座中，这种索引被称为“排名”（rank）。

此外，幻灯片指出“排名”的概念可以比简单的索引更为一般化，不一定需要像 C 语言那样通过指针来实现，即数组的索引不必直接通过地址偏移来获取。这样的表述有助于理解在不同编程环境下如何灵活地实现和理解向量或数组的结构。

这张幻灯片进一步详细介绍了向量抽象数据类型（ADT）的基本特性和操作。向量是基于数组的具体数据类型（CDT），可以存储一系列任意对象。向量中的元素可以通过其“排名”进行访问、插入或移除，这里的“排名”指的是该元素之前的元素数量。如果指定了错误的排名（例如负数排名），则会抛出异常。

此外，幻灯片列出了向量的主要操作，包括：

1. **elemAtRank(r)**：返回排名为 r 的元素，但不移除它。
2. **replaceAtRank(r, o)**：将排名为 r 的元素替换为对象 o，并返回原先的元素。
3. **insertAtRank(r, o)**：在排名为 r 的位置插入一个新元素 o。
4. **removeAtRank(r)**：移除并返回排名为 r 的元素。

还提到了其他一些操作，如 size() 和 **isEmpty()**，用以返回向量的大小和检查向量是否为空。这些操作使得向量在使用时更加灵活和强大。

这张幻灯片介绍了如何将向量作为栈（Stack）使用。在栈的数据结构中，元素的添加和移除通常发生在同一端，即遵循“后进先出”（LIFO）的原则。

幻灯片中描述的具体操作包括：

1. **push(o)**：相当于调用 insertAtRank(size(), o)，将新元素插入向量的末尾。这里的 size() 函数返回当前向量的大小，即最大排名值，因此新元素总是被放在现有元素之后。
2. **pop()**：相当于调用 removeAtRank(size() - 1)，从向量的末尾移除元素。这里使用 size() - 1 是因为排名是从 0 开始计算的，所以最后一个元素的排名是当前大小减一。

此外，幻灯片还提到使用向量作为栈在特定情境下非常有用，如从文件中读取未知数量的元素时。这是因为栈允许在不知道元素总数的情况下灵活地添加和移除元素。

这张幻灯片探讨了向量的应用场景，突出了向量与传统固定大小数组的区别和优势。向量的一个主要特点是没有自动的存储大小限制，这使得它们比固定大小的数组更加灵活和适用于更广泛的场景。

直接应用：

• 有序对象集合：向量可以用来存储和管理有序的对象集合，例如在基本数据库中使用。这种用法利用了向量动态调整大小的特性，便于实现元素的插入和删除操作。

间接应用：

• 辅助数据结构：在许多算法中，向量常用作辅助数据结构，比如用来存储额外的信息或临时数据。
• 其他数据结构的组件：向量还可以作为更复杂数据结构的组成部分，例如用于构建图的邻接列表等。

通过这些应用，可以看出向量不仅仅是一种简单的数据存储方式，它的灵活性和扩展性使其成为实现复杂数据管理和处理任务的理想选择。

这张幻灯片详细介绍了基于数组的向量实现方式。在这种实现中，向量是通过一个固定大小的数组 V 来实现的，数组的大小为 N。这种向量实现还涉及到一个变量 n，用于追踪向量当前存储的元素数量，即向量的实际大小。

关键操作：

• **elemAtRank(r)**：该操作允许在 O(1) 时间复杂度内通过简单地返回数组索引 V[r] 来访问排名为 r 的元素。这种实现利用了数组的随机访问能力，即直接通过索引访问任意位置的元素。

幻灯片下方的图表显示了数组 V 的结构，其中从 0 到 n-1 的索引部分表示向量当前存储的元素，而 n 到 N-1 的部分则为空（未使用）。这样的视觉表示帮助理解向量如何在数组的基础上动态调整其内容的存储。这种实现虽然依赖于数组的固定大小，但通过管理变量 n，向量能够有效地提供动态添加或删除元素的功能。

插入操作：

• 当在向量中的特定排名 r 处插入一个新元素 o 时，需要首先为新元素腾出空间。这是通过将从排名 r 到 n-1 的元素向前移动一位来实现的，其中 n 是插入前向量中的元素数量。
• 在最坏的情况下（即 r=0），需要移动整个数组的所有元素，因此这种插入操作的时间复杂度是 O(n)。

删除操作：

• 删除操作中，当从排名 r 处移除一个元素时，需要通过将从排名 r+1 到 n-1 的元素向后移动一位来填补被移除元素留下的空位。
• 同样，在最坏的情况下（r=0），需要移动整个数组的所有元素，因此删除操作的时间复杂度也是 O(n)。

在幻灯片的图示中，你可以看到具体的元素如何在数组中移动以完成插入和删除操作。这些操作虽然在单个操作层面上可能较为耗时，但它们是向量灵活性的基础，允许向量在任何位置进行元素的增加或删除。对于频繁进行这类操作的应用场景，可能需要考虑其他更优化的数据结构来降低操作成本。

这张幻灯片总结了基于数组的向量实现在性能方面的关键特点。

空间和时间复杂度：

• 数据结构使用的空间为 O(n)，其中 n 是数组的大小。
• size、isEmpty、elemAtRank 和 replaceAtRank 这些操作的时间复杂度为 O(1)，因为它们可以直接通过数组索引来访问或替换元素，不需要遍历或移动其他元素。
• insertAtRank 和 removeAtRank 操作的时间复杂度为 O(n)，因为这两种操作可能需要移动从插入或删除点开始的所有后续元素，以保持元素的连续性。

栈操作性能：

• push 和 pop 操作通常具有 O(1) 的时间复杂度，因为它们只涉及在数组的末端添加或移除元素，不需要移动数组中的其他元素。
  • 但是，如果在执行 push 操作时数组空间不足，需要对数组进行扩容（即分配更大的数组并复制现有元素到新数组），这时 push 的时间复杂度将依赖于数组的当前大小。
• pop 操作在不需要调整数组大小的情况下始终为 O(1)。

动态调整数组大小：

• 在执行 insertAtRank 操作时，如果数组已满，幻灯片提到不会抛出异常，而是选择将数组替换为一个更大的数组。这种动态调整大小的策略有助于向量适应不断变化的数据需求，虽然在扩容时会有较大的时间成本，但可以避免因固定大小限制而无法添加更多元素的问题。

这些性能特点和设计决策都体现了基于数组的向量在处理动态数据集时的灵活性与效率，特别是在频繁进行末端操作（如栈操作）的应用场景中。

这张幻灯片详细介绍了基于数组的向量在空间不足时如何增长（动态调整大小），以及相关的策略和考虑因素。

动态扩容策略：

• 当进行 push 操作（相当于 insertAtRank(n)）时，如果数组已满（即 n 等于 V.length - 1），则需要扩大数组以容纳更多元素。这种情况下，不会抛出异常，而是创建一个更大的数组。
• 扩容的操作涉及将所有现有元素从旧数组复制到新数组，这个过程的时间复杂度为 O(n)，因为需要逐个复制所有元素。

新数组的大小策略：

• 增量策略（Incremental Strategy）：每次扩容时增加一个常数 c。这种策略可以根据具体需要逐步增加空间，但可能导致频繁的扩容操作和较高的长期复制成本。
• 加倍策略（Doubling Strategy）：每次需要扩容时将数组大小加倍。这种策略虽然在每次扩容时需要移动更多的数据，但减少了扩容的频率，通常在多次操作中平均下来会更高效。

扩容算法实现示例：

• 如果数组已满（n 等于数组长度减一），则创建一个新的更大的数组 A。
• 将旧数组 V 的所有元素复制到新数组 A。
• 更新指向数组的引用，使 V 指向新数组 A。
• 将新元素 o 插入到数组的末尾（索引 t 处）。
• 更新当前元素计数 n。

这种基于数组的可增长向量实现提供了灵活的数据结构选择，适应不同的应用需求，同时也考虑了性能和空间效率的平衡。

这张幻灯片探讨了在基于数组的向量中，针对动态扩容采取的两种策略——增量策略和加倍策略——的比较。

策略比较：

• 幻灯片中分析了在进行一系列 n 次推入（push）操作时，这两种策略所需的总时间 ( T(n) )。这里的“推入”指的是在数组的末尾添加一个元素，将数组视作一个栈。
• 假设初始时从一个空栈开始，该栈由一个大小为1的数组表示。

摊销时间：

• 摊销时间是对一系列操作中每次操作的平均时间进行计算。在这里，摊销时间定义为 ( \frac{T(n)}{n} )，即对 ( n ) 次操作的总时间 ( T(n) ) 进行平均。

摊销分析帮助我们理解在重复执行相同操作时，某些成本高昂的操作（如数组扩容）的平均成本是如何随着操作次数的增加而变得相对较小的。对于增量策略，由于每次只增加固定的大小，当元素填满时需要频繁扩容，因此可能会有较高的摊销成本。对于加倍策略，尽管单次扩容的成本较高，但由于扩容的频率降低，使得整体摊销成本相对较低。

通过比较这些策略，可以更好地理解不同场景下选择合适的动态数组策略的重要性，以及如何平衡操作的即时性能与长期效率。

这张幻灯片进一步讨论了在摊销分析中对操作序列的处理及其意义：

分析摊销成本：

• 假设某个单独的操作，如 push，在最坏情况下需要时间 T。
• 如果执行一系列的 s 个这样的操作，那么最坏情况下的总时间是 sT，这是时间上的一个上限。

摊销时间的重要性：

• 尽管 sT 是可能的总时间上限，但实际上这种最坏情况可能并不会发生。因此，总时间 ( T_s ) 可能实际上远小于 sT，即可能是 o(sT)，这里的“o”表示小于但不是渐进严格小于。
• 实际中更关注的是每次操作的平均时间 ( \frac{T_s}{s} )，这反映了在给定操作序列中，每次操作的平均成本。

实际应用示例：

• 例如，在需要将长序列的元素推入向量的情况下，如从文件中读取数据，单次操作的摊销成本提供了对操作效率的更实际的评估。

通过摊销分析，我们能够更准确地理解在连续多次操作中，由于扩容等高成本操作的偶发性，平均每次操作的成本实际上可能远低于单次独立操作的最坏情况成本。这种理解有助于开发者在设计数据结构和算法时做出更合理的选择和优化。

这张幻灯片提出了一个问题：“摊销分析与平均情况分析有什么不同？” 并给出了解释：

摊销分析与平均情况分析的区别：

1. 摊销分析：

   • 摊销分析关注的是一系列操作的总成本，并将这个成本平均分摊到每个操作上。这种分析方法考虑的是特定操作序列中的依赖性，通常是在最坏情况下的一长串实际操作。
   • 摊销分析特别适用于评估那些偶尔需要大量资源（如时间或空间）的操作，但在整个操作序列中这种高成本操作不频繁发生。

2. 平均情况分析：

   • 平均情况分析评估所有可能操作的平均表现。它通常假设每个操作的发生概率相同，或者依据特定的概率分布来计算。
   • 这种分析忽略了操作之间的依赖性，每个操作被视为独立的。

核心区别：

• 摊销分析提供了在特定情况下，特定操作序列总体上的性能评估。它不考虑操作的独立性，而是作为一个整体来看待。
• 平均情况分析则考虑每个操作独立发生的平均效果，适用于操作独立且概率已知的场景。

简而言之，摊销分析和平均情况分析都试图提供操作成本的一个有效估计，但摊销分析着重于实际操作序列的整体成本，而平均情况分析则着重于理论上每个操作的平均表现。这两种方法在数据结构和算法的设计与评估中各有其适用场景。

这张幻灯片解释了如何用大O记号描述摊销成本，并澄清了一些常见的误解：

大O记号的应用：

• 大O记号常用于描述算法的时间复杂度，它不仅仅局限于描述算法的最坏情况。大O记号可以用来描述任何函数，包括算法的平均情况、最好情况或任何特定情况的复杂度。

摊销成本的描述：

• 在摊销分析中，大O记号同样适用。这里的关键区别在于，我们关注的是操作序列的整体成本而非单个操作。
• 我们可以区分两种成本度量：
  • 序列操作的最坏情况成本：指整个操作序列中每个操作的平均最坏情况成本，这种成本考虑了整个操作序列。
  • 单个操作的最坏情况成本：传统的方法，通常考虑单一操作在最坏情况下的成本。

摊销成本的实际意义：

• 通过摊销分析，我们可以更合理地评估数据结构或算法在长期运行中的性能。例如，在使用动态数组时，尽管单次扩容可能很耗时，但平均到每次操作（如添加元素），成本可能相对较低。
• 使用大O记号描述这些成本可以帮助我们更好地理解和预测程序的行为，尤其是在处理复杂和连续操作的场景中。

总之，摊销成本的描述使我们能够从更宏观的角度评估和理解算法或数据结构在实际使用中的表现，而大O记号为这种分析提供了一个清晰和统一的方法论。

这两张幻灯片通过一个具体的例子说明了增量策略下向量扩容的摊销成本分析：

增量策略示例：

• 起始容量为3，每次容量增加3（即 ( c = 3 )）。在这个示例中，我们可以观察到每当数组满时，就进行扩容操作，新增的容量为3。
• 每次扩容操作的成本为复制所有现有元素的成本（即 n 的值），加上插入新元素的成本。

具体的操作和成本：

• 在幻灯片中，对一系列的 push(0) 操作进行了详细说明。对于每次操作，都标明了当前的数组状态、数组大小 ( n ) 和具体的操作成本。
• 在这个例子中，每次 push 操作的基本成本为1（即插入操作本身的成本）。当数组需要扩容时，成本会突增，例如：
  • 第4次 push 操作需要将数组容量从3增加到6，操作成本为 ( 3（复制成本）+ 1（插入成本） = 4 )。
  • 第7次 push 操作将容量从6增加到9，操作成本为 ( 6（复制成本）+ 1（插入成本） = 7 )。

成本分析：

• 根据增量策略，大约有1/3的 push 操作需要进行扩容（每次扩容后，可以进行额外的两次 push 操作而无需扩容）。
• 因此，虽然大多数 push 操作的成本为1，但扩容操作的成本很高，导致每次 push 操作的平均成本为 ( O(n) )。

这个示例很好地说明了增量策略的问题：尽管扩容不是每次操作都会发生，但当发生时其成本非常高，从而提高了整体操作的平均成本。这也突出了为什么在实际应用中，例如实现动态数组时，其他策略（如加倍策略）可能更受青睐，因为它们可以更有效地分摊高成本操作，降低平均成本。

这张幻灯片进一步详细地分析了增量策略下的时间复杂度，提供了一个数学模型来计算摊销成本。

增量策略分析：

• 在增量策略下，假设每次数组扩容都增加固定数量 ( c ) 的容量，数组将被替换 ( k = \frac{n}{c} ) 次，其中 ( n ) 是总的操作数。
• 每次替换的成本等于当前数组的大小，因此总成本是 ( n + c + 2c + 3c + \ldots + kc )。

成本的计算：

• 上述序列可以重新写作 ( n + c(1 + 2 + 3 + \ldots + k) )。
• 利用求和公式 ( 1 + 2 + 3 + \ldots + k = \frac{k(k + 1)}{2} )，我们得到 ( n + c\frac{k(k + 1)}{2} )。
• 因为 ( k = \frac{n}{c} )，所以 ( n + c\frac{k(k + 1)}{2} ) 可以进一步简化为与 ( n^2 ) 成正比的形式。

时间复杂度：

• 因此，整个操作序列的总时间 ( T(n) ) 是 ( O(n^2) )，这反映了随着操作数量的增加，总成本的平方级增长。
• 摊销时间，即平均每次操作的成本，则为 ( O(n) )，这远高于不需要扩容时每次 push 的 ( O(1) ) 成本。

总结：

• 增量策略虽然简单，但由于每次扩容的成本与当前数组大小成正比，导致在操作数较多时效率低下。
• 这种策略在需要频繁扩容的应用场景下表现不佳，因为它会显著增加每次操作的平均成本，尤其是在大量数据操作时。

幻灯片通过数学分析清晰地表明了为什么在设计具有动态大小的数据结构时，可能需要考虑更高效的扩容策略，例如加倍策略，以优化性能和成本。

这张幻灯片通过一个实例解释了在动态数组中使用加倍策略的摊销成本计算。加倍策略意味着每当数组满时，其容量将加倍，这是一种常用于动态数组扩容的高效策略。

加倍策略示例：

• 初始容量为3，每次数组满时容量加倍。成本模式如下：普通 push 操作成本为1，每次扩容时的成本为当前数组的大小。
• 在此示例中，成本序列为：1, 1, 1, 3+1, 1, 1, 6+1, 1, 1, 1, 1, 1, 12+1, 等等。
• 扩容成本依次为3, 6, 12…等等，每次都是上一次容量的两倍。

摊销成本分析：

• 每次扩容的成本随着数组大小线性增加，但由于容量加倍，扩容的频率迅速降低。在每次扩容后，更多的 push 操作可以以常数成本执行，直到下一次扩容。
• 因此，随着操作数 ( n ) 的增加，需要扩容的 push 操作占总操作的比例呈指数级减少。

平均成本计算：

• 初始 ( n ) 次 push 的总成本是一个由常数和每次扩容成本组成的序列。考虑到扩容成本是前一次容量的大小，每次加倍意味着总成本是 ( 3 + 3 \times 2 + 6 \times 2 + \ldots )，即每次扩容前容量的总和。
• 摊销成本可以近似计算为 ( \frac{T(n)}{n} )，其中 ( T(n) ) 是总成本。因为扩容的频率随 ( n ) 的增加而减少，随着 ( n ) 的增加，摊销成本逐渐趋近于常数 ( O(1) )。

这个示例展示了加倍策略相较于增量策略的优势：虽然每次扩容的成本更高，但由于加倍后可容纳更多元素，使得扩容频率降低，从而在大量操作下显著降低了平均成本。这种策略非常适合那些元素数量动态增长的场景，如在处理不确定数量的数据输入时。

这两张幻灯片进一步展示了在使用加倍策略时对于摊销成本的分析和解释，特别是如何将扩容成本均摊到单个操作上。

加倍策略的具体成本分析：

• 起始容量为2，每次数组满时容量加倍。成本序列包括每次推入操作的基本成本（1）和每次扩容操作的额外成本（例如第二次操作的成本是2+1，第四次操作的成本是4+1）。
• 这些成本序列显示，虽然扩容操作的成本较高（因为它包括复制现有所有元素的成本），但这些高成本的操作随着操作序列的推进变得越来越稀疏。

摊销成本的计算：

• 每次扩容操作后，因为容量加倍，可以进行更多的 push 操作而不需要再次扩容，从而使得之后的多次 push 操作的成本保持在常数级别（O(1)）。
• 第二张幻灯片通过一个视觉示例展示了如何将扩容的成本均摊到随后的每个 push 操作上。红色成本表示已经被摊销的部分，这表明扩容的成本可以被视为在随后的许多操作中均摊。

摊销成本的效果：

• 由于加倍策略允许在每次扩容后进行大量的操作，因此即使扩容本身的成本高，摊销后的平均成本仍然是O(1)。
• 这种策略的优势在于，尽管初期和每次扩容时成本较高，长远来看，整体的操作成本逐渐趋于常数，提高了操作效率。

总的来说，加倍策略在动态数组的实现中是高效的，因为它减少了扩容的频率并优化了摊销成本，从而使得平均每次操作的成本降低，这对于处理大规模数据非常有利。

这张幻灯片进一步分析了使用加倍策略时的摊销成本，具体考察了对于 ( n ) 次 push 操作，数组增长的次数及总的时间复杂度。

加倍策略的核心分析：

• 在这个分析中，假设 ( n ) 是2的幂次方。这种假设简化了计算，因为每次数组容量加倍时，都是从更小的2的幂次方增长到下一个2的幂次方。
• 在这种情况下，数组被替换的次数 ( k ) 将是 ( \log_2 n )。这是因为每次加倍都相当于数组容量的指数增长。

操作的总时间 ( T(n) )：

• 总时间包括每次 push 的基本成本和每次扩容时复制元素的成本。
• 如果考虑到每次扩容，我们有 ( 1 + 2 + 4 + 8 + \ldots + 2^{k-1} ) 的成本序列，其中 ( 2^{k-1} ) 是最后一次扩容时的容量，恰好小于 ( n )。
• 这个序列是一个等比数列，其和可以通过公式 ( 2^k - 1 ) 计算，其中 ( k = \log_2 n )，因此序列的和是 ( n - 1 )。

总的摊销成本：

• 因此，整个操作序列的总时间 ( T(n) ) 大致为 ( n + (n - 1) = 2n - 1 )，简化为 ( O(n) )。
• 这意味着平均每次 push 操作的摊销成本是 ( O(1) )，即使考虑到所有的扩容成本，每次操作的平均成本仍然保持常数。

通过这种方式，加倍策略不仅简化了管理动态数组的复杂性，而且通过有效分摊较高的扩容成本，确保了整体操作效率的提升，这使得加倍策略成为实现动态数组时一种非常高效的策略。

这两张幻灯片进一步说明了加倍策略的具体例子和动态数组的增长过程。

第一张幻灯片：加倍次数示例

• 这张幻灯片展示了当 ( n ) 是1, 2, 和4时，数组需要加倍的次数和对应的 ( \log_2 n ) 的值。
• 例如：
  • 当 ( n = 1 ) 时，不需要加倍，( \log_2 1 = 0 )。
  • 当 ( n = 2 ) 时，需要加倍一次，( \log_2 2 = 1 )。
  • 当 ( n = 4 ) 时，需要加倍两次，( \log_2 4 = 2 )。
• 这些例子很好地说明了加倍策略中数组容量增长的对数关系。

第二张幻灯片：动态数组操作示例

• 这张幻灯片通过 ( n = 4 ) 的具体示例详细描述了动态数组在加倍策略下如何操作。
  • 起始时，容量为1，大小为0。
  • 第一次 push(A)，不需要扩容。
  • 第二次 push(B)，容量不足，进行一次加倍（扩容到2），需要复制1个元素。
  • 第三次 push(C)，再次容量不足，进行加倍（扩容到4），需要复制2个元素。
  • 第四次 push(D)，此时无需扩容，直接添加。
• 这个过程演示了每次达到容量限制时如何进行加倍和元素复制。

这些例子有助于理解加倍策略在实际操作中如何执行，以及每次操作的成本如何被计算。通过观察每次加倍后新的空间如何允许更多的 push 操作而无需立即再次扩容，可以清晰地看到摊销成本分析的实际应用。这种策略虽然在短期内可能看起来成本较高，但长远来看，由于加倍的效率，整体成本是非常合理的。

这张幻灯片进一步深入解释了使用加倍策略时的时间复杂度分析。

分析摘要：

• 在加倍策略中，每次数组容量满时加倍，如果假设 ( n ) 是操作总数并且每次操作都可能触发加倍，则总加倍次数 ( k ) 是 ( \log_2 n )。
• 每次加倍的成本是当前数组的大小，所以成本序列是 ( 1, 2, 4, \ldots, 2^{k-1} )。

总时间 ( T(n) )：

• 计算所有操作的总成本（包括每次 push 操作和扩容成本），可以得出总时间 ( T(n) ) 等于基本 push 操作的成本 ( n ) 加上每次扩容的成本之和 ( 1 + 2 + 4 + \ldots + 2^{k-1} )。
• 根据等比数列求和公式，( 2^{k-1} ) 的求和结果是 ( 2^k - 1 )，其中 ( 2^k = 2^{\log_2 n} = n )，所以求和结果是 ( n - 1 )。
• 因此，总时间 ( T(n) ) 为 ( n + (n - 1) = 2n - 1 )，简化后得到 ( O(n) )。

摊销成本：

• 摊销每次 push 操作的成本，即平均每次操作的成本，为 ( \frac{T(n)}{n} )，简化得 ( O(1) )。这说明尽管有时需要进行成本较高的扩容操作，平均到每个 push 上的成本仍然保持常数级别。
• 这表明，在考虑所有必要的内存分配时，单次 push 的摊销成本与预先分配所有所需内存的成本相当。

结论：

• 使用加倍策略的动态数组，即使考虑到最坏情况下的扩容成本，其摊销操作成本也是 ( O(1) )，使得它在实践中非常高效。
• 大O记号隐藏了由于扩容造成的常数倍的额外成本，但即便如此，这种策略因其高效的摊销成本而被广泛采用。

这张幻灯片提出了一些用于讨论或作为练习的问题，旨在探讨不同的数组增长策略及其适用场景。

讨论问题与练习：

1. 何时可能更愿意使用增量增长而非加倍增长？

   • 在某些场景下，如果内存资源较为有限或昂贵，使用增量增长策略可能更为合适。这是因为加倍策略虽然减少了扩容次数，但每次扩容时可能会浪费更多的内存，尤其是在数组元素数量巨大时。
   • 此外，如果数组增长的预测非常稳定或增长速度较慢，增量增长可以避免过度分配未使用的内存空间，从而更加节约资源。

2. 为什么是加倍而不是三倍或其他常数因子增长？

   • 加倍增长是一种平衡了扩容次数和每次扩容代价的策略。如果使用三倍或更大的增长因子，虽然可以进一步减少扩容的频率，但这会在每次扩容时创建更多未使用的空间，可能导致内存使用效率降低。
   • 从理论上分析，加倍策略（因子为2）提供了一个折中的选择，既能有效减少扩容操作的次数，又能控制因大量未使用空间造成的内存浪费。

3. 尝试用任意增长因子 ( b ) 重新进行分析

   • 分析不同的增长因子 ( b ) 对摊销成本和内存效率的影响。这个练习可以帮助理解不同增长策略在长期操作成本和内存使用效率上的权衡。
   • 例如，可以计算当增长因子为 ( b ) 时，总的摊销成本如何随着 ( b ) 的变化而变化，并探讨在什么条件下，某个特定的 ( b ) 值可能比加倍策略更优。

实践建议：

• 对于这些讨论问题和练习，实际编写和测试代码实现不同的数组增长策略将是非常有益的。通过实际应用，可以更直观地观察到不同策略在性能和资源利用上的差异，从而为选择最适合特定应用需求的策略提供数据支持。

这张幻灯片提供了一些关于在 C 或 C++ 中实现动态数组（向量）扩容策略时的技术建议。

优化动态数组扩容策略：

1. **使用 realloc 而不是 malloc 或 new**：

   • 在 C/C++ 中，动态数组的扩容可以通过 realloc 函数来优化。realloc 试图调整已分配内存块的大小，它有可能直接在现有内存块的后面扩展空间，避免了复制整个数组到新位置的需要。
   • 相比之下，使用 malloc 或 new 分配一个新的更大的内存块后，通常需要手动复制旧数组的内容到新内存块，然后释放旧内存块，这增加了复制的开销。

2. 使用 memcpy 进行数据复制：

   • 如果 realloc 需要移动内存块（当无法在原地扩展时），使用 memcpy 可以直接复制整个内存块，这比逐个复制数组元素更快。
   • memcpy 是直接操作内存的方式，它通常由底层优化实现，可以提供比循环逐一复制元素更高效的数据复制性能。

技术选择的影响：

• 性能提升：使用 realloc 和 memcpy 可以显著提高动态数组在扩容时的性能，尤其是在元素数量较多的情况下。
• 内存管理：这种方法简化了内存管理，减少了内存碎片，因为它尽量在原地扩展内存，减少了内存分配和释放的次数。

通过这些优化，可以使 C/C++ 中的动态数组扩容更加高效，从而提升整体应用程序的性能。这种优化对于实现需要高效内存使用和快速响应时间的系统（如大数据处理和实时系统）尤为重要。

Lecture15 (Priority Queues & Heaps)

1. 抽象数据类型（ADT）：

   • 抽象数据类型是关于定义数据类型的接口而不涉及实现细节的概念。
   • 它关注的是数据类型对外展现的行为，也就是从外部看到的功能和行为。
   • 抽象数据类型定义了所提供的方法，并可能对这些方法的复杂度有要求，比如某个操作必须在O(n)的时间复杂度内完成。

2. 具体数据类型（CDT）：

   • 具体数据类型则涉及到数据结构和算法的具体实现。
   • 它关注的是从内部看到的行为，也就是数据类型的内部逻辑和实现方式。

总的来说，抽象数据类型提供了一个理论框架，定义了数据类型应该有的操作和性能要求，而具体数据类型则是这些理论在具体应用和编程中的实现。

这张图片解释了抽象数据类型（ADT）和具体数据类型（CDT）的实用性，以及它们在面向对象编程中的标准应用：

1. 规范与实现的分离：

   • 这一原则帮助将数据类型的“规范”（即接口）与其“实现细节”分开。这意味着可以独立于实现来定义接口的行为。

2. 允许不同的CDT实现同一个ADT：

   • 这种分离使得可以为同一个ADT探索不同的CDT实现。例如，一个列表（List）的ADT可以通过数组或链表的CDT来实现。

3. 快速替换或改进CDT而无需更改ADT的使用者代码：

   • 由于ADT的定义与CDT的具体实现无关，因此可以在不影响使用已有ADT代码的情况下，更换或优化其背后的CDT。

4. 需要注意的是ADT和CDT的命名差异：

   • 在实际应用中，ADT和CDT可能有不同的命名方式，开发者在使用和实现时需要区分这些名称，以避免混淆。

这些特点体现了在面向对象设计中，抽象和具体实现分离的重要性，旨在提高代码的灵活性、可扩展性和可维护性。

这张图片介绍了优先队列抽象数据类型（Priority Queue ADT）的特点和操作方法：

1. 优先队列的结构：

   • 优先队列存储一个条目集合，每个条目是一对键值对（key, value）。

2. 主要方法：

   • insert(k, v)：插入一个带有键 k 和值 v 的条目。
   • removeMin()：移除并返回键最小的条目。注意，与Map不同，优先队列通常不需要一个查找特定键的find(k)方法。

3. 附加方法：

   • min()：返回但不移除键最小的条目。
   • size()：返回队列中的条目数量。
   • isEmpty()：检查队列是否为空。

4. 应用场景：

   • 待命乘客（例如在航空公司的候补登机名单中）
   • 拍卖中的出价排序
   • 股票市场中的订单优先处理
   • 打印队列管理

优先队列是一种常用的数据结构，适用于需要按特定顺序处理条目的场景，其中条目的处理优先级由键值决定。

这张图片介绍了两种简单的优先队列具体数据类型（CDT）的实现方式，即使用未排序列表和使用已排序列表的实现方式，以及各自的性能特点：

1. 使用未排序列表实现：

   • 结构：元素在列表中的位置是随机的，例如列表 [4, 5, 2, 3, 1]。
   • 性能：
     • insert(k, v)：插入操作可以在 O(1) 时间内完成，因为可以直接将元素添加到列表的头部或尾部。
     • removeMin() 和 min()：需要遍历整个列表以找到键最小的元素，因此这两个操作的时间复杂度为 O(n)。

2. 使用已排序列表实现：

   • 结构：元素按键值排序存放，例如列表 [1, 2, 3, 4, 5]。
   • 性能：
     • insert(k, v)：插入操作需要 O(n) 时间，因为需要找到适当的位置来保持列表的排序。
     • removeMin() 和 min()：由于最小元素总是在列表的头部，这两个操作可以在 O(1) 时间内完成。

图片最后还提出了一个练习问题，探讨在实现时使用单链表是否足够，或者是否需要双链表。这个问题的答案取决于具体的应用需求和对操作效率的要求。使用双链表可能会简化某些操作，如在列表中间插入或删除节点，但同时也会增加额外的空间复杂度。

Heap

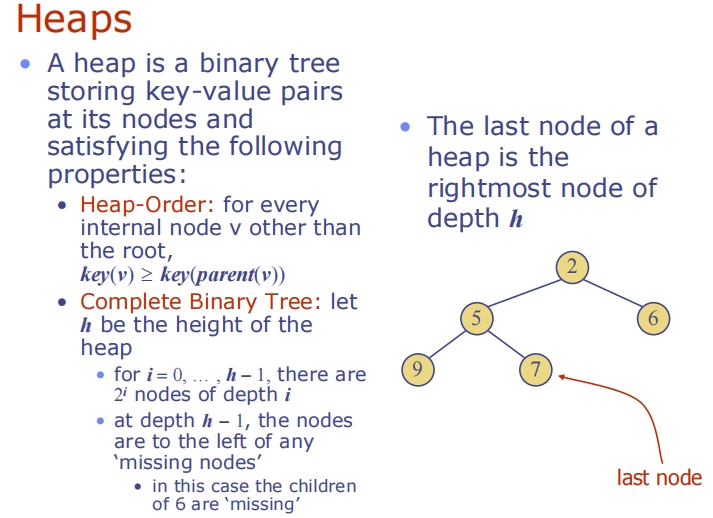
这张图片解释了堆（Heaps）的基本概念，这是一种特殊的二叉树，用于在计算机科学中管理优先队列：

1. 堆的定义：

   • 堆是一种存储键值对的二叉树。
   • 每个节点的键值都大于或等于其父节点的键值，这称为堆的顺序属性（Heap-Order）。

2. 完全二叉树：

   • 堆是一种完全二叉树，这意味着除了最后一层外，其他每层都被完全填满，且所有节点都向左对齐。
   • 对于堆的任何给定深度 i，该深度将有 2^i 个节点（直至最后一层）。

3. 堆的结构特征：

   • 最后一个节点是堆中深度为 h（堆的高度）的最右侧节点。

堆通常用于实现优先队列，因为它允许快速的访问、删除最小元素（或最大元素，具体取决于堆的类型），同时也能高效地插入新元素。如图中所示，堆确保了在 O(log n) 的时间复杂度内完成插入和删除最小元素的操作，这是由其树状结构和堆属性共同保证的。

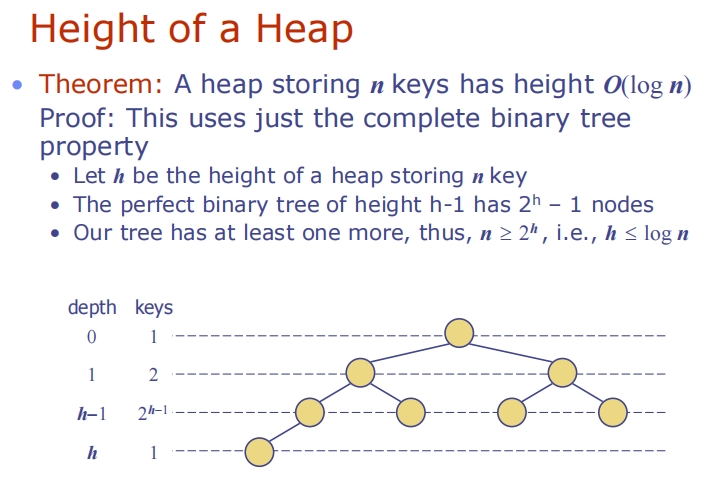
这张图片提供了一个关于堆高度的定理及其证明，这是理解堆性能的关键：

定理：

• 一个存储 ( n ) 个键的堆具有高度 ( O(\log n) )。

证明：

• 假设堆的高度为 ( h )。
• 完美二叉树的定义是每一层都被完全填满的二叉树。一个高度为 ( h-1 ) 的完美二叉树将有 ( 2^h - 1 ) 个节点。
• 由于堆是一种完全二叉树，所以在高度 ( h ) 的堆至少还有一个节点（最少情况是堆的最后一层只有一个节点），因此 ( n ) 至少等于 ( 2^h )。
• 根据这种关系，可以得出 ( h \leq \log n )。

图片中的图示显示了各个深度层的节点数，其中每个深度 ( i )（从0到 ( h-1 )）的节点数是 ( 2^i )，并且在深度 ( h ) 至少有一个节点。这个视觉表现帮助理解堆的结构以及如何快速推导出它的高度。

这个定理说明了堆的高效性，特别是在执行插入或删除操作时，因为这些操作通常涉及到沿树的路径移动，其复杂度与树的高度直接相关。由于堆的高度是对数级的，所以相关操作也能在对数时间内完成，这是堆数据结构在多种应用中非常有价值的原因之一。

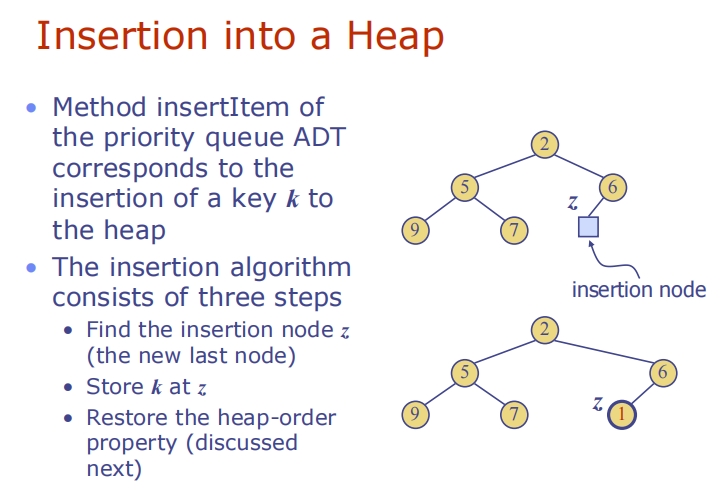
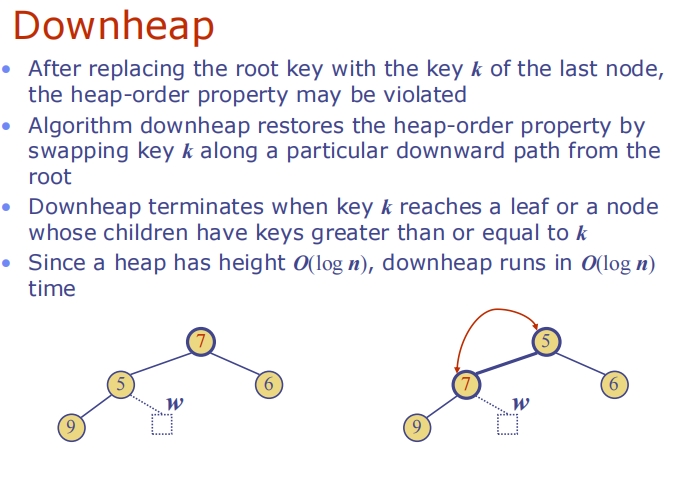
Insertion into a Heap

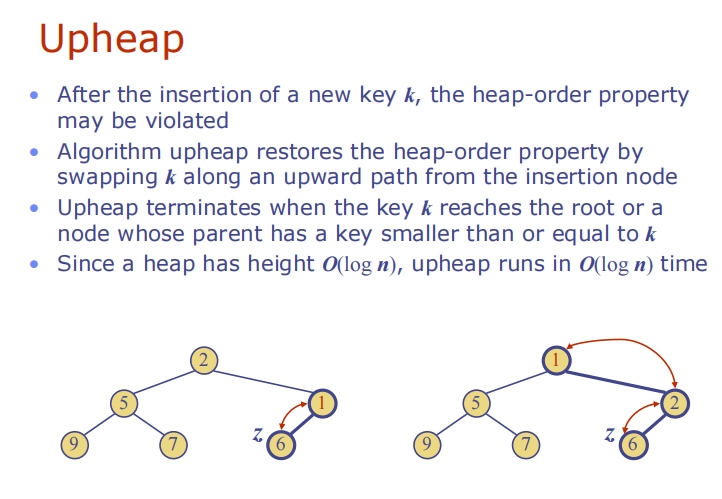
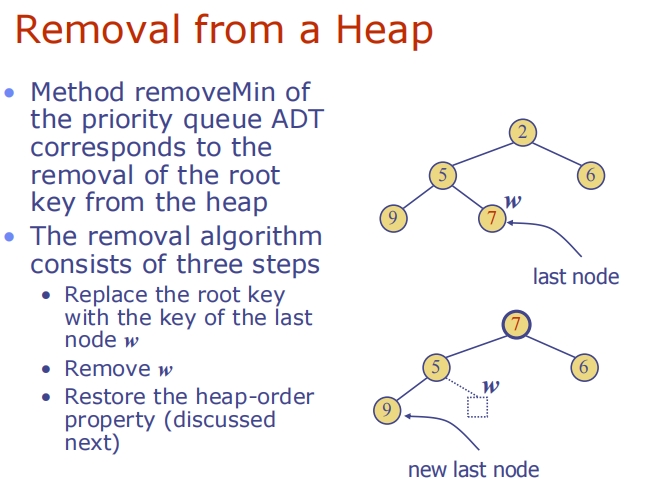
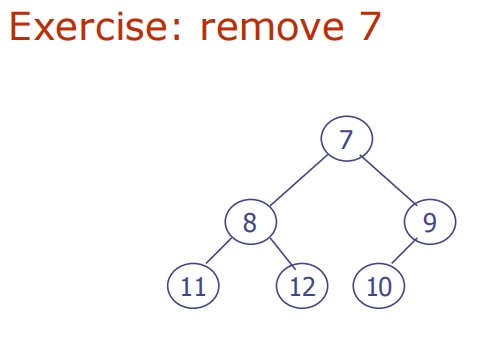
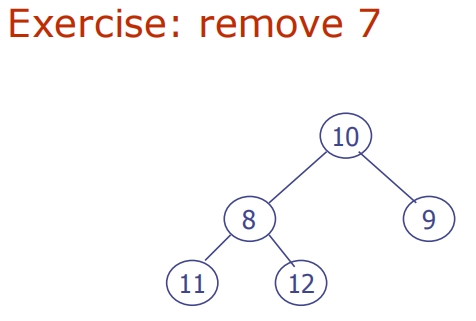
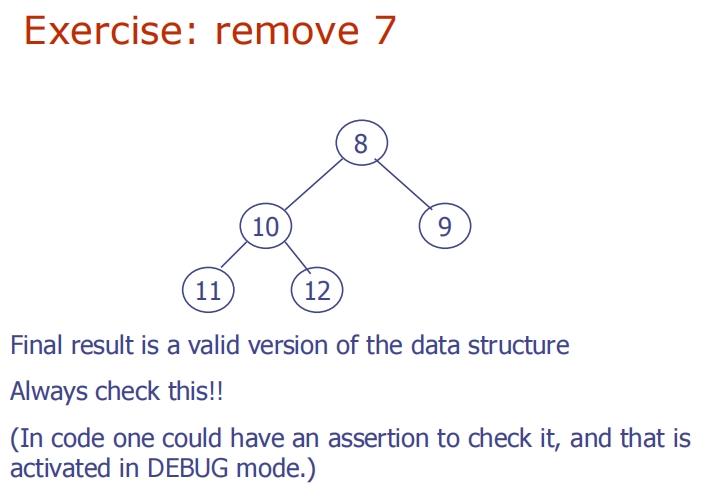
Removal from a Heap

Array Heap Implementation

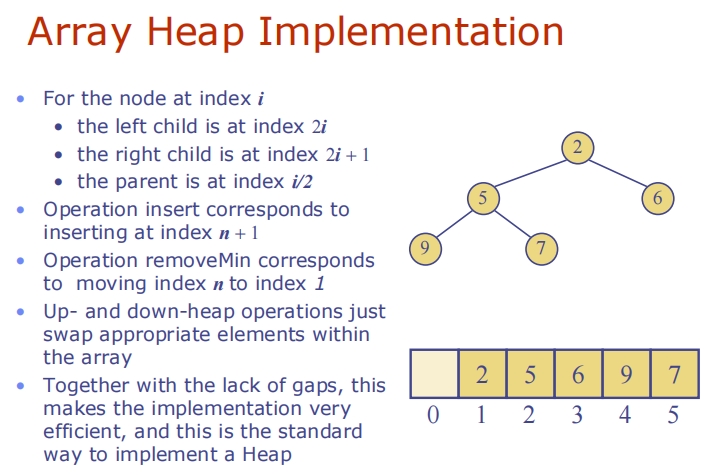
这两张图片介绍了如何使用数组来实现堆的数据结构：

1. 数组表示法：

   • 可以用一个数组（或向量）来表示一个堆，数组的长度是 ( n+1 )，其中 ( n ) 是堆中的元素数量。
   • 节点间的链接不是显式存储的。而是通过数组的索引来隐式表示节点之间的关系。

2. 节点位置关系：

   • 对于数组中的任何位置 ( i )：
     • 左子节点的索引是 ( 2i )。
     • 右子节点的索引是 ( 2i+1 )。
     • 父节点的索引是 ( i/2 )（整除）。
   • 索引 0 通常不被使用，这是为了使索引计算更加方便和快捷。

3. 操作的数组实现：

   • 插入操作：新元素被插入到数组的末尾（即索引 ( n+1 )）。
   • 删除最小元素（removeMin）：通常涉及将数组的第一个元素（根元素）与最后一个元素交换，然后在数组的开始部分重构堆结构。
   • 上浮（up-heap）和下沉（down-heap）操作：通过在数组中适当交换元素来维护堆的性质。

4. 效率：

   • 由于数组的连续存储方式和堆的结构特性，数组实现的堆非常高效。这种没有“间隙”的实现使得堆操作非常迅速，是实现堆的标准方法之一。

这种实现方式不仅节省了存储空间（因为不需要额外的指针或链接存储），而且由于内存的连续使用，也能提高缓存的效率。因此，数组实现的堆在实际应用中非常普遍，特别是在需要优先队列的数据结构中。

Lecture16 (Map ADT : using lists)

这张图片概述了映射（Maps）这一抽象数据类型（ADT）的特征和操作：

1. 映射的定义：

   • 映射是一种模拟键值对集合的数据结构，其中可以通过键来搜索条目。

2. 主要操作：

   • 搜索（Search）：根据键来查找对应的值。
   • 插入（Insert）：添加一个新的键值对到映射中。
   • 删除（Delete）：移除映射中的一个键值对。

3. 键的唯一性：

   • 在一个标准的映射中，每个键只能出现一次，不允许有重复的键。
   • 如果需要存储多个相同的键对应不同的值，可以使用“多映射”（Multi-map）。

映射是计算机科学中非常基础且广泛应用的数据结构，用于存储和管理大量的数据，其中每项数据都能通过一个唯一标识符（键）快速访问。常见的实现方式包括哈希表、搜索树等。

这张图片描述了映射（Map）这一抽象数据类型（ADT）的关键方法，详细阐述了如何操作键值对：

1. **get(K k)**：

   • 如果映射中有键为 ( k ) 的条目，则返回其对应的值；如果没有，返回 null。

2. **put(K k, V v)**：

   • 将条目 ( (k, v) ) 插入到映射中。
   • 如果键 ( k ) 在映射中已存在，则替换原有的值，并返回被替换的旧值；如果不存在，返回 null。

3. **remove(K k)**：

   • 如果映射中有键为 ( k ) 的条目，移除该条目并返回其对应的值；如果没有，返回 null。

4. **size() 和 isEmpty()**：

   • size() 返回映射中的条目数量。
   • isEmpty() 判断映射是否为空。

5. **keys()**：

   • 返回映射中所有键的可迭代集合。

6. **values()**：

   • 返回映射中所有值的可迭代集合。

7. **entries()**：

   • 返回映射中所有键值对的可迭代集合。

这些方法提供了映射的基本功能，允许用户通过键来有效地存取和管理数据。映射的这些操作是许多编程任务中数据处理的基础，特别是那些需要快速数据查找、数据关联和数据更新的应用。

这张图片强调了在使用二叉树结构时不要混淆两种主要用途：优先队列（Priority Queue, PQ）与映射（Map），以及它们的实现方式：堆（Heaps）和二叉搜索树（Binary Search Trees, BST）。

1. 优先队列和堆：

   • 优先队列通常使用堆来实现，堆是一种特殊的二叉树，它保持父节点的键总是小于（或大于）其子节点的键，这样堆的根节点总是最小（或最大）键。
   • 优先队列主要支持快速访问并删除最小（或最大）键的操作。

2. 映射和二叉搜索树：

   • 映射可以使用二叉搜索树来实现。二叉搜索树是一种有序的树，其中每个节点的左子树只包含键小于该节点键的节点，右子树只包含键大于该节点键的节点。
   • 映射允许基于任意键快速访问、插入和删除条目，而不仅仅是最小或最大键。

3. 关键区别：

   • 访问方式：在优先队列中，你通常只能访问最小（或最大）键，而在映射中，你可以访问任意键。
   • 用途差异：优先队列主要用于任务调度、事件驱动模拟等需要按特定顺序处理元素的场景。映射则广泛用于需要大量查找、插入和删除操作的应用，如数据库和存储系统。

图片的目的是提醒我们在设计和选择数据结构时要注意这些差异，确保选择最适合当前应用需求的结构。

这张图片描述了使用列表（链表）实现映射（Map）的简单方法，以及如何优化获取映射大小的操作：

1. 列表实现映射：

   • 实现映射的一种直观方式是使用链表，可以是单向链表或双向链表。
   • 链表中的每个节点存储一个键值对，链表的遍历操作用于执行查找、插入和删除等操作。

2. 维护大小计数器：

   • 为了优化获取映射大小的操作，单独存储一个大小计数器 n，记录映射中元素的数量。
   • 通过这种方式，getSize() 操作可以在 O(1) 时间复杂度内完成，因为不需要遍历整个链表来计算元素数量。
   • 每次添加或删除元素时，更新这个计数器以保持其准确性。

使用链表来实现映射的优点是实现简单直观，但主要的缺点是查找、插入和删除操作的时间复杂度通常是 O(n)，因为可能需要遍历整个链表。这种实现方式适合元素数量较少的情况。对于需要频繁查找操作的大型数据集，使用如哈希表或二叉搜索树的更高效数据结构可能更为合适。

这张图片进一步阐述了基于列表的映射（Map）实现及其性能考虑：

1. 操作的时间复杂度：

   • 由于在列表（无论是未排序还是已排序）中进行操作（如查找、插入和删除）通常需要遍历列表，这些操作的时间复杂度为 O(n)。

2. 未排序列表的适用性：

   • 对于元素数量较少的映射，使用未排序的列表实现是可行的，因为虽然操作是线性时间，但对于小规模数据来说，这种差异不会太显著。

3. 使用已排序列表的考量：

   • 虽然使用已排序的列表可以提高某些操作的效率（例如最小或最大元素的快速访问），但对于映射来说，这并没有根本上提高性能，因为需要能够访问任意键的值，而不仅仅是最小或最大键。
   • 即使列表是有序的，查找、插入和删除任意键的平均时间复杂度仍然是 O(n)，因为可能需要遍历整个列表来找到特定的键。

总的来说，列表基础的映射实现简单易于理解，但由于其性能限制，主要适用于小规模数据集。对于需要高效查找、频繁更新或大规模数据处理的应用，更复杂的数据结构如哈希表或平衡二叉搜索树（例如 AVL 树、红黑树）可能更为适合。

Lecture17 (Map ADT and hashtables)

Lecture19 (Binary Search Trees)

BST 即二叉搜索树（Binary Search Tree），是一种特殊的二叉树，用于快速查找、插入、删除数据的数据结构。二叉搜索树具有以下基本特性：

1. 节点的排列：每个节点包含一个键及其关联的值，并且每个节点都有两个区分的子节点，通常称为左子节点和右子节点。
2. 有序性：
   • 对于树中的任意节点，其左子树中的所有节点的键都小于该节点的键。
   • 右子树中的所有节点的键都大于该节点的键。
3. 操作效率：在理想的情况下（树保持平衡），查找、插入、删除操作的时间复杂度可以达到 O(log n)，其中 n 是树中节点的数量。这是因为每进行一次比较，就可以排除一半的可能性。
4. 中序遍历有序：对二叉搜索树进行中序遍历（先遍历左子树，然后访问根节点，最后遍历右子树）将按升序访问所有节点的键。

使用场景

二叉搜索树广泛用于实现各种数据结构，如集合、映射（字典）等，其中需要频繁地查找和更新数据。

优点

• 动态数据结构：二叉搜索树是动态的，可以根据需要通过添加或删除节点来扩展或收缩，无需预先知道数据量的大小。
• 中等复杂度操作：提供了比较均衡的操作性能，尤其是在维持平衡的情况下。

缺点

• 可能退化：如果插入的元素是有序的（例如递增或递减顺序），二叉搜索树可能退化成一个链表，此时所有操作的时间复杂度退化为 O(n)。
• 维护成本：为了保持树的平衡，可能需要通过旋转等操作来调整树的结构，如 AVL 树和红黑树等平衡二叉搜索树。

二叉搜索树因其结构简单和较好的平均性能表现，而被广泛应用于软件开发中，特别是在需要频繁查找和有序排列数据的场景。

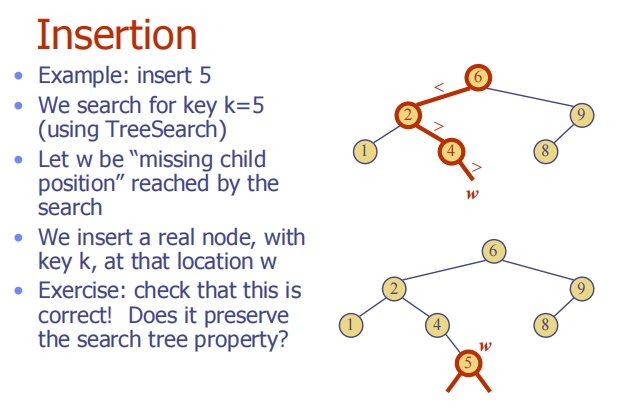
Insertion

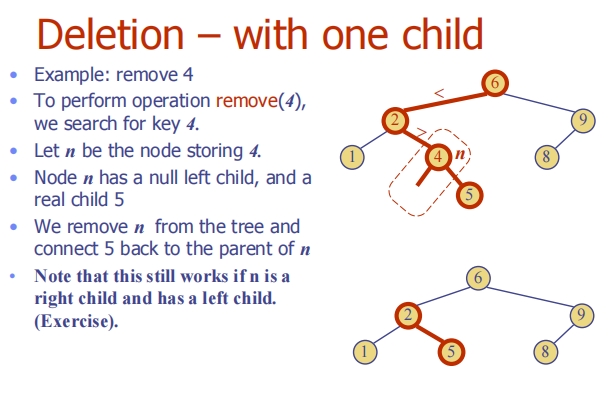
Deletion

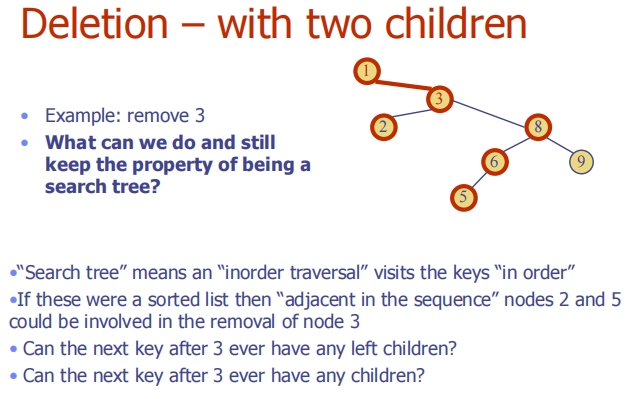
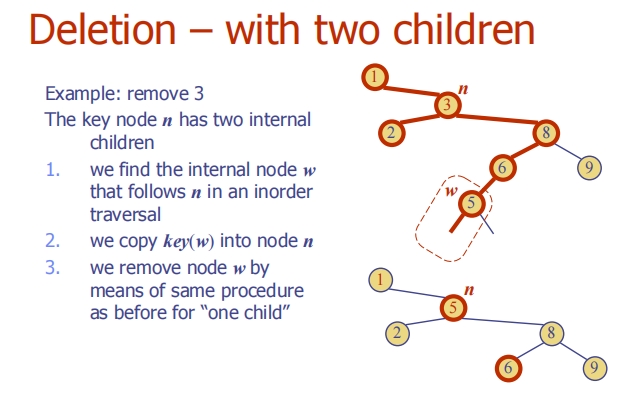
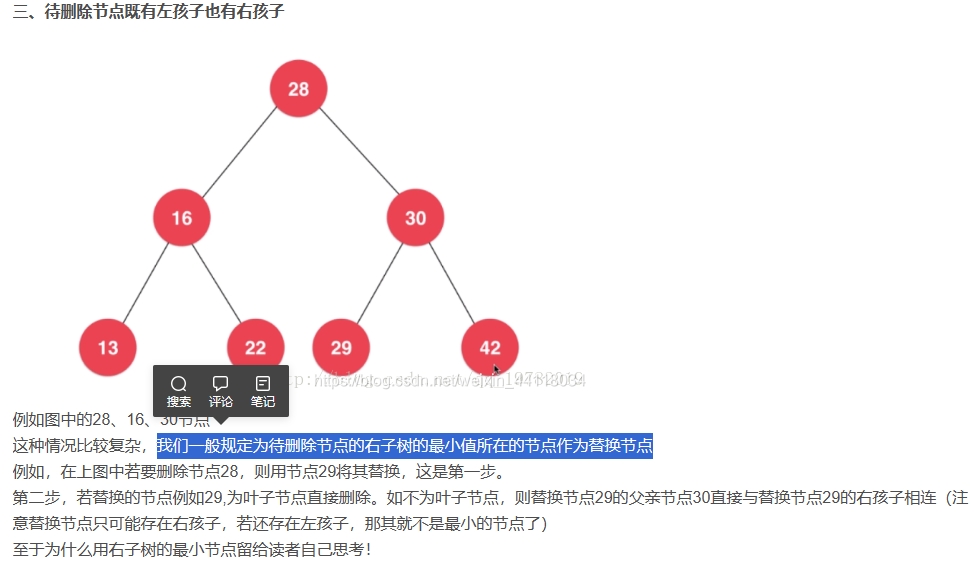
Lecture20 (Brute force, D&C, heuristics and “Dynamic Programming”)

Dynamic Programming (DP)

这张图片介绍了一个使用动态规划（DP）解决子集和问题的具体方法。这个方法用一个布尔数组来追踪可能达到的子集和。这里是具体的说明：

动态规划算法

• 算法概念：考虑集合中的每个数一次，同时跟踪到目前为止哪些子集和是可能的。
• 操作步骤：对于集合中的每个数，更新布尔数组，以反映包含这个数后可能达到的新的和。

主要数据结构

• 布尔数组 Y：这个数组的大小为 ( K+1 )（其中 ( K ) 是目标和），用于存储布尔值。
  • Y[m] = true 表示存在一个子集，其元素和正好为 ( m )。
  • 数组的索引对应于可能的和，从 0 到 ( K )。

更新布尔数组的方法

1. 初始化：Y[0] 设置为 true，因为和为0总是可以通过不取任何元素来实现。
2. 遍历集合中的每个数：对于集合中的每个数 ( x )，从 ( K ) 向下到 ( x ) 遍历数组 Y。
3. 更新数组：如果 Y[j - x] 是 true（这意味着存在一个子集其和为 ( j-x )），那么设置 Y[j] 为 true。这反映了加上当前考虑的数 ( x ) 后，可以达到和为 ( j ) 的新子集。

算法的效果

通过这种方式，当处理完所有的数后，Y[K] 的值如果为 true，则表示存在一个子集，其元素之和为目标和 ( K )；如果为 false，则表示不存在这样的子集。

这种动态规划方法有效地利用了空间和时间，能够比较高效地解决问题的大小和目标和适中的子集和问题。不过，需要注意的是，这种方法的空间复杂度为 ( O(K) )，如果 ( K ) 很大，可能需要较大的内存空间。

这张图片描述了子集和问题的另一种动态规划解法，称为 DP for Subset Sum 2。此方法同样使用布尔数组追踪可达成的和，但强调了如何在已知较小子集和的基础上，逐步添加元素以探索更大子集和的策略。

方法概述

• 基本思想：假设已经找到了所有由元素 x[0] 到 x[i-1] 组成的子集和的可能性。现在的目标是考虑加入 x[i] 后，如何影响这些和。
• 递推策略：如果已知某个和 m 可以由 x[0] 到 x[i-1] 的某个子集得到，那么显然，通过添加 x[i]，可以得到新的和 m + x[i]。

步骤详解

1. 迭代每个元素：对于集合中的每个元素 x[i]，更新可能达到的和。
2. 更新可能和：
   • 遍历所有可能的和 m 从大到小（重要，以避免在同一迭代中重复使用相同元素）。
   • 如果 dp[m] 为 true（表示可以通过之前的元素组合得到和为 m），则将 dp[m + x[i]] 设置为 true。

为何从大到小更新

从大到小更新是为了确保每个元素在每一轮中只被计算一次。这样可以防止一个元素被重复加入，影响结果的正确性。例如，如果我们从小到大更新，那么在处理到较大的 m 时，可能会错误地使用了在当前迭代已更新的 dp 值，从而导致某些和被错误地认为是可达的。

应用和效果

• 这种方法在逻辑上直接且易于实现，特别适合处理问题规模较小或中等的子集和问题。
• 它通过递归地添加新元素，并更新可能的和，使得我们可以构建出一个完整的可能和的图景。
• 尽管在最坏情况下，时间复杂度仍然是指数级（因为必须考虑集合的所有可能子集），但动态规划提供了一种相对高效的方法来探索和记录解决方案的路径，特别是当和 K 较小或数据规模适中时。

这两张图片介绍了动态规划方法解决子集和问题的时间复杂度，并对其进行了比较分析。

Complexity 1

• 外层循环：遍历每个元素，复杂度为 (O(n))。
• 内层循环：遍历布尔数组 (Y)，长度为 (K+1)，复杂度为 (O(K))。
• 总体复杂度：由于每个元素的添加需要遍历整个数组 (Y)，所以总体复杂度是 (O(nK))。
• 与 (O(2^n)) 比较：动态规划的复杂度 (O(nK)) 比穷举法的 (O(2^n)) 要好很多。穷举法需要检查每个可能的子集，而子集的数量随集合大小指数增长。

Complexity 2

• 隐藏的指数：虽然表面上复杂度是 (O(nK))，但如果 (K) 非常大（尤其是在 (K) 是输入大小的多项式时），这个复杂度实际上隐含了指数性质。
• 输入大小：如果 (K) 用二进制表示，需要的比特数 (B) 是 (O(\log K))。
• 实际复杂度：考虑到 (K) 的二进制表示，复杂度可以重新表示为 (O(n 2^B))，这是一个伪多项式时间复杂度，因为它依赖于数字 (K) 的大小，而非其比特数。
• 伪多项式时间：这种复杂度虽然比 (O(2^n)) 好，但仍然依赖于 (K) 的实际值，而不仅仅是其大小，这在某些情况下可以接近指数复杂度。

结论

动态规划方法为子集和问题提供了一种相对有效的解决策略，特别是当 (K) 不是极端大的值时。然而，这种方法的复杂度随 (K) 的大小而变化，特别是在 (K) 很大时，可能仍然需要显著的计算资源。因此，虽然它比简单的穷举方法有效，但在处理大规模问题时仍需谨慎。

Min-Coins version

这张图片进一步讨论了动态规划方法在最少硬币找零问题中的应用，特别是“DP for Min-Change-Giving 2”。这个方法的核心在于累积到目前为止的最佳解答，并在此基础上考虑新的硬币如何影响已有的解答。

方法概述

• 基本思想：假设已经找到了使用硬币 x[0], ..., x[i-1] 的最优解。现在，引入新的硬币 x[i]，并探讨其如何影响能达到的总金额及使用的硬币数量。

算法步骤

1. 已知解：如果已知某金额 m 可以用 x[0] 到 x[i-1] 的组合达到，并且用了 c 枚硬币。
2. 添加新硬币：通过考虑新的硬币 x[i]，可以尝试形成新的金额 m + x[i]。
   • 如果使用硬币 x[i] 后可以形成新金额，则更新该金额所需的最少硬币数量为 min(current, c + 1)，其中 current 是不使用 x[i] 时的硬币数。

实现逻辑

• 使用一个数组，通常命名为 dp，其中 dp[j] 表示达到金额 j 所需的最小硬币数。
• 初始时，dp[0] 设置为 0（因为金额0不需要硬币），其他金额设置为一个很大的数（如无穷大），表示尚未找到有效的硬币组合。
• 对于每个硬币 x[i] 和每个可能的金额 j（从硬币值 x[i] 到总金额 K），更新 dp[j]。

性能分析

• 时间复杂度：依然是 (O(nK))，其中 n 是硬币种类数，K 是目标金额。
• 空间复杂度：(O(K))，需要一个大小为 K+1 的数组来存储中间结果。

算法的优点

• 灵活性：可以灵活处理各种硬币和金额组合，适用于多种变化的金额和硬币种类。
• 精确性：能够准确找到达成特定金额所需的最小硬币数。

应用场景

这种动态规划策略非常适合于需要精确控制资源使用的场合，例如自动售货机的找零系统、金融应用中的最优资金配置等。

i是索引，x[i]是i索引上的面值

• Y[m] = true iff some subset has been found that sums to m

Lecture21 (Minimum Spanning Trees)

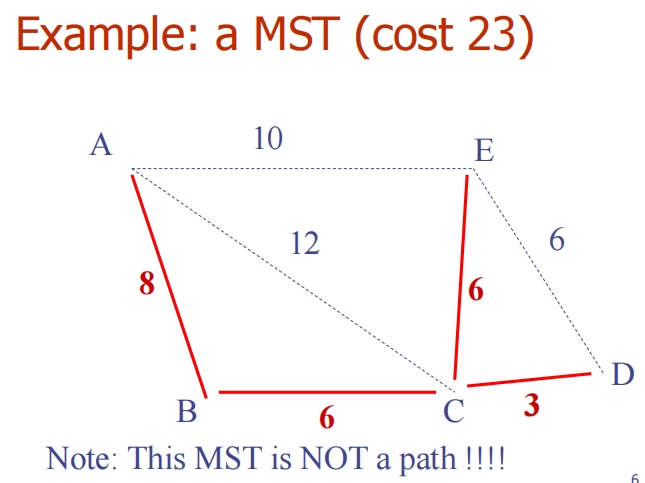
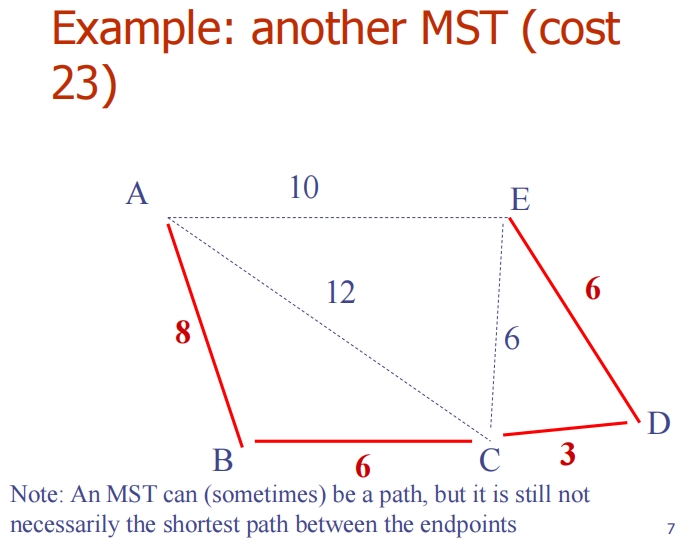
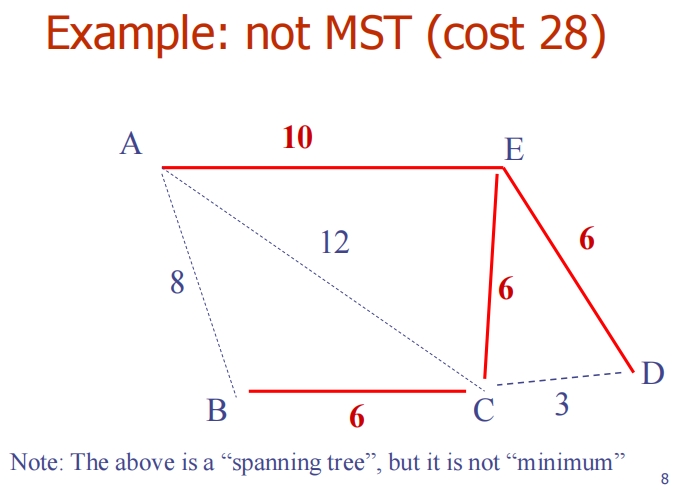
Prim’s algorithm

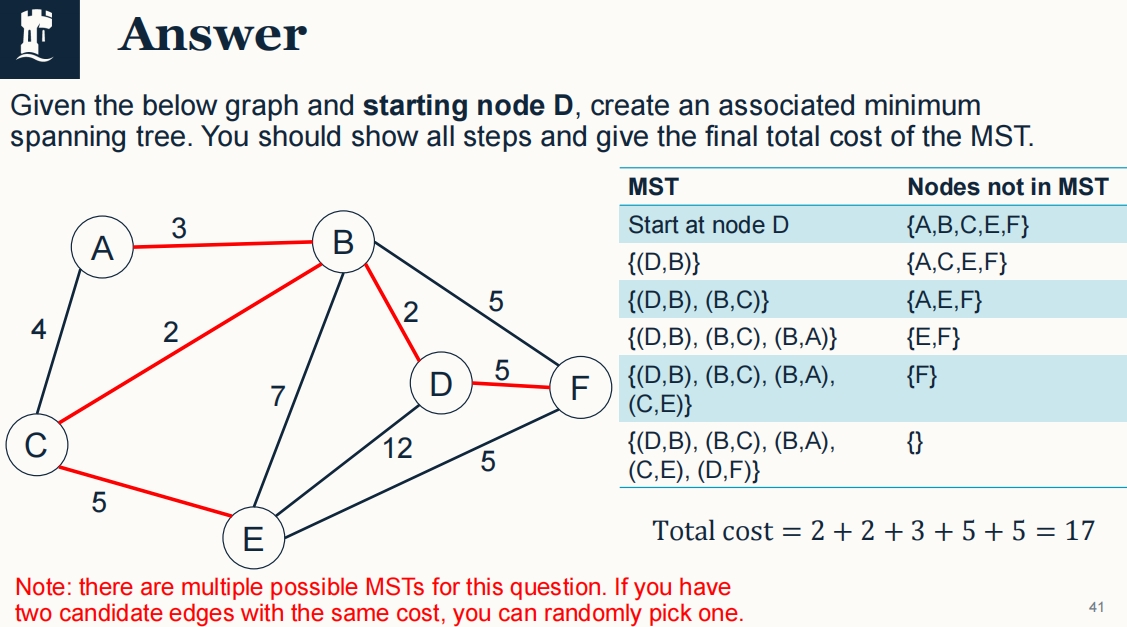
这张图片介绍了普里姆算法（Prim’s Algorithm），这是一种用于构造最小生成树（MST）的著名算法。最小生成树是一种在给定图中包含所有顶点且边的总权重最小的树形结构。

普里姆算法的步骤如下：

1. 选择起始顶点：

   • 从图中选择任意一个顶点作为起始点 ( M )。

2. 选择最短边：

   • 从顶点 ( M ) 出发，找到连接 ( M ) 和图中任何其他未包含在当前最小生成树中的顶点 ( N ) 的最短边。

3. 添加边到 MST：

   • 将找到的最短边 ( (M, N) ) 添加到最小生成树中。

4. 重复选择和添加边：

   • 继续选择当前最小生成树中任一顶点到任一非树顶点的最短边，重复这个过程，直到图中所有顶点都被包含在最小生成树中。

5. 处理多个最短边的情况：

   • 如果存在多条具有相同长度的最短边，可以选择其中任意一条进行添加。

算法特点：

• 贪心算法：普里姆算法是一种贪心算法，它在每一步都选择当前看起来最优的选择（即最短的边），以期达到全局最优的解决方案。
• 复杂度：算法的时间复杂度依赖于实现方式，常见的实现如使用优先队列可以达到 (O(E \log V))，其中 (E) 是边的数量，(V) 是顶点的数量。
• 适用性：适用于稠密图，因为其对边的选择是全局性的，每次都需要从大量的边中选择最小边。

普里姆算法广泛应用于网络设计、电路布局设计等领域，其中需要最小化布线长度或者构建成本。

Lecture22

这张图片介绍了二叉搜索树（Binary Search Tree, BST）的基本概念。二叉搜索树是一种具有键值对节点的二叉树，满足以下“搜索树”属性：

• 对于树中的任何节点（不仅限于根节点），其左子树中的所有节点的键都严格小于该节点的键。
• 其右子树中的所有节点的键都严格大于该节点的键。

因此，对二叉搜索树进行中序遍历（in-order traversal）时，可以按照键的增序访问所有键。这意味着遍历首先访问左子树，然后是当前节点，最后是右子树，这样可以得到一个有序的键序列。

这张图片描述了二叉搜索树（BST）中的不平衡问题。图片中展示了两棵具有相同内容但结构不同的二叉搜索树，它们的中序遍历结果都是1,2,3,4,5，但树的高度不同。

• 左边的树呈现为一条线，高度为4，因为每个节点（除最后一个外）都只有一个右子节点。
• 右边的树更加平衡，其高度为2，结构较为均衡，每个节点的左右子树的高度差不大。

不平衡的二叉搜索树会影响其操作的效率，因为二叉搜索树的一些基本算法的时间复杂度依赖于树的高度。理想情况下，树的高度应该接近log(n)，其中n是树中节点的数量。当树高度接近于线性时（如左边的树），许多操作的效率会显著降低。

为了解决这个问题，可以使用自平衡的二叉搜索树，例如AVL树或红黑树，它们通过旋转操作在插入和删除节点时保持树的平衡，从而保证树的高度大约是log(n)。这样可以确保树的操作效率更高，更加稳定。

这张图片探讨了自平衡二叉搜索树的一些问题和挑战。主要内容包括：

1. 不平衡树的问题：

   • 如果一个搜索树非常不平衡，虽然总有可能重构成一个平衡的树，但这样的重构可能需要处理整棵树的所有节点，其时间复杂度为 (O(n))，这样的效率与理想的 (O(\log n)) 相比非常低。

2. 重平衡的需求：

   • 重平衡操作的理想时间复杂度应该是 (O(\log n)) 或 (O(\text{height}))，这意味着重平衡操作应该局限于影响到的路径，而不是整棵树。这样可以有效减少操作的复杂度，使树的维护更高效。

3. 重平衡的实现可能性：

   • 在不知道具体的实现机制之前，不一定显而易见可以仅通过修改最近变更节点的路径来实现树的重平衡。

这张图片的核心观点是，虽然理论上可以通过完全重建来平衡一个非常不平衡的搜索树，但这种方法效率低下。实际上，更高效的策略是通过局部调整（如旋转操作），仅在树的某个部分（通常是插入或删除节点后影响到的路径）进行调整，以实现快速有效的重平衡。这是自平衡树（如AVL树和红黑树）的基本工作原理。

这张图片进一步探讨了二叉搜索树（BST）不平衡问题的解决策略。主要内容概括如下：

1. 总重建的问题：

   • 对于任何数量的节点，理论上总是存在一个平衡的二叉搜索树。完全重建一个树（即重新安排所有节点以形成一个平衡的二叉树）是一个可能的解决方案，但这需要 (O(n)) 时间，这与BST应有的 (O(\log n)) 效率相违背。

2. 小范围局部重建的目标：

   • 为了保持BST的效率，目标是在插入或删除操作时进行小范围的局部重建。这种方法意在通过只对受影响的局部区域进行调整，而不是对整个树进行重建，从而维持树的平衡。

3. 探讨小范围局部重建的可能性：

   • 本讲座的内容将围绕“我们可以做哪些小范围的局部重建？”这一问题展开，探讨在插入或删除节点时如何有效地调整树的结构，以避免大规模的重建，保持操作的高效性。

通过使用这种策略，可以避免在每次操作后都进行全树的重建，从而确保BST操作的时间复杂度理想地保持在 (O(\log n))。这种策略的实际应用包括AVL树和红黑树中的旋转操作，这些操作都是为了在局部范围内快速恢复树的平衡。

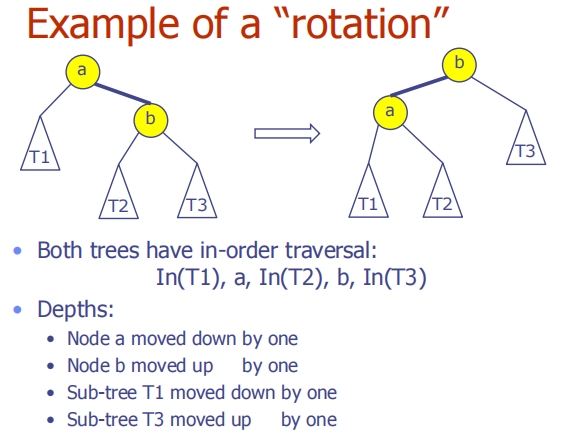
这两张图片解释了二叉搜索树（BST）的一个示例以及在其中进行的“旋转”操作的影响。

第一张图片 - BST 示例

• 图中展示了一个包含节点a和b的BST，其中a是根节点，b是右子节点。
• 该树包含三个子树：T1、T2和T3，它们每一个都是BST。
• 树的高度计算为：h(T) = max(1 + h(T1), 2 + h(T2), 2 + h(T3))。
• 中序遍历（In-order traversal）的结果是：In(T1), a, In(T2), b, In(T3)。

第二张图片 - 旋转操作示例

• 展示了对BST进行一次旋转操作前后的变化。在这个例子中，b被旋转到根的位置，而a则移动到了左子树的位置。
• 旋转操作保持了树的中序遍历结果不变，仍然是：In(T1), a, In(T2), b, In(T3)。
• 旋转后，a的深度下降了一层，而b上升到了根的位置。子树T1的位置下降一层，T3的位置上升一层。

旋转的意义

• 旋转操作是自平衡二叉搜索树中一个关键的机制，它用于维持或改善树的平衡，从而保证操作的高效性，尤其是在插入或删除节点后。
• 这种局部修改保持了整体结构的搜索效率，避免了进行全树的重建。
• 此操作通常在AVL树或红黑树中看到，这些树种通过局部旋转自动保持或恢复平衡，以维持操作的最优时间复杂度 (O(\log n))。

这些图示帮助理解BST在结构修改时如何通过局部变动维持全局效率和顺序，是理解自平衡机制的重要基础。

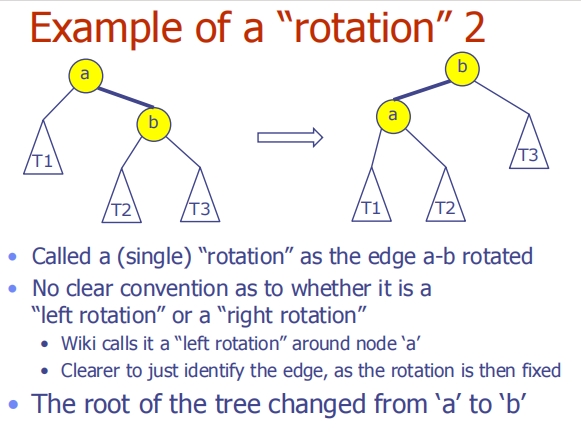
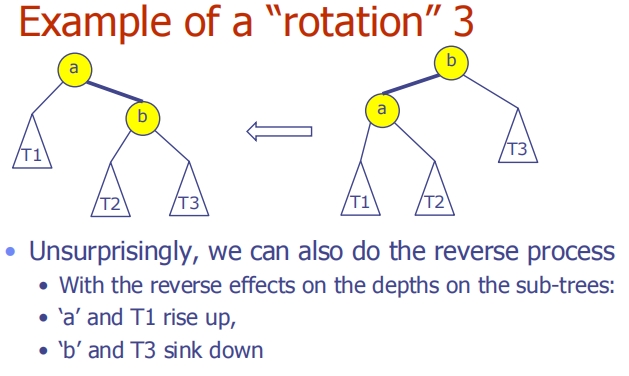
这三张图片进一步解释了二叉搜索树中旋转操作的细节和分类，特别是区分左旋和右旋。

第一张图片 - 旋转操作的描述

• 这张图片描述了在二叉搜索树中进行的单一旋转操作，即节点b围绕节点a进行旋转。文中提到没有清晰的共识来确定这是左旋还是右旋，不同的来源可能会有不同的说法。例如，维基百科可能将其称为围绕节点a的“左旋”。
• 图片建议更清晰的方式是直接指定需要旋转的边，因为这样旋转的方向就被固定了。
• 在这次旋转后，树的根从a变为b。

第二张图片 - 反向旋转的示例

• 展示了旋转操作的反向过程，即可以将旋转后的树恢复到旋转前的状态。这个操作说明了旋转是可逆的。
• 反向旋转的效果是深度的相反变化：a和T1上升，而b和T3下降。

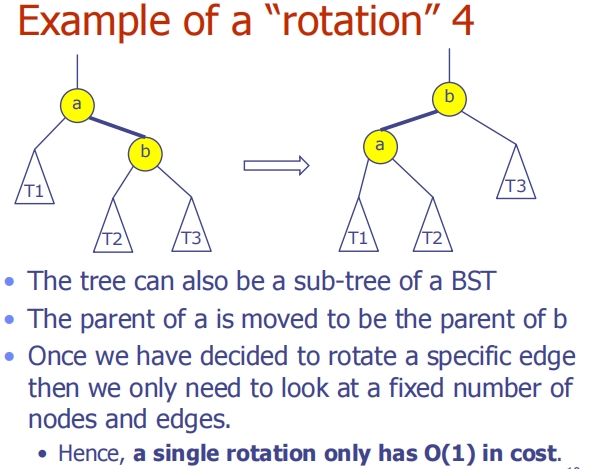
第三张图片 - 旋转操作的成本和影响

• 这张图片强调了旋转操作可以看作是在固定数量的节点和边上进行的操作，因此其成本是常数时间，即O(1)。
• 图片还说明了旋转操作不仅可以应用于整个树，还可以应用于二叉搜索树的任何子树。这意味着无论在树的哪个部分，旋转都可以有效地用来调整子树的结构，而不影响整体的中序遍历结果。

这一系列图片清晰地说明了BST中的旋转操作如何用于保持或恢复树的平衡，尤其是在插入或删除操作后，这是自平衡二叉搜索树（如AVL或红黑树）维持效率的关键机制。

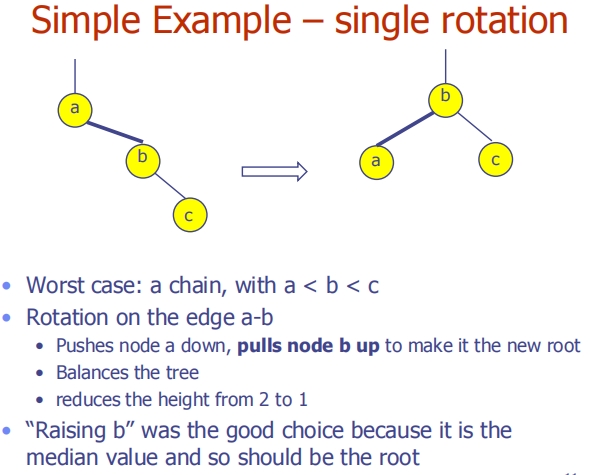
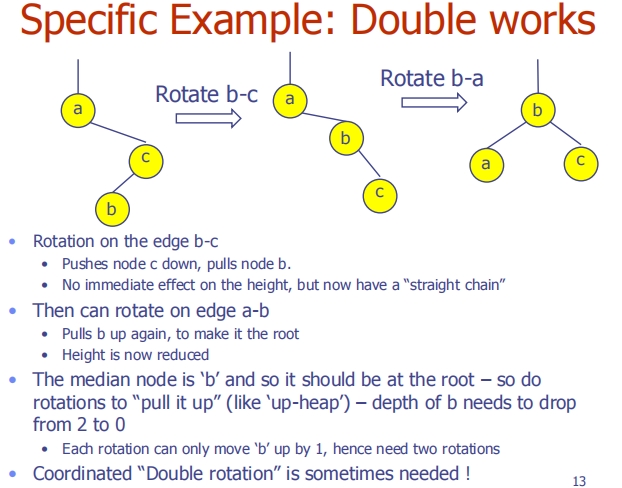
这三张图片逐步说明了在二叉搜索树中旋转操作的不同情况，包括单一旋转和双重旋转，以及这些操作如何影响树的结构和高度。

第一张图片 - 简单例子：单一旋转

• 展示了一个链式结构的二叉搜索树（最坏情况），节点a、b和c按照升序排列。
• 通过将b旋转到根位置，将a下降到左子节点，而将c保持为右子节点，可以有效地减少树的高度，从2降到1。
• 这种旋转被认为是有用的，因为b是中位数，理论上应该是根节点，这样可以最大化平衡。

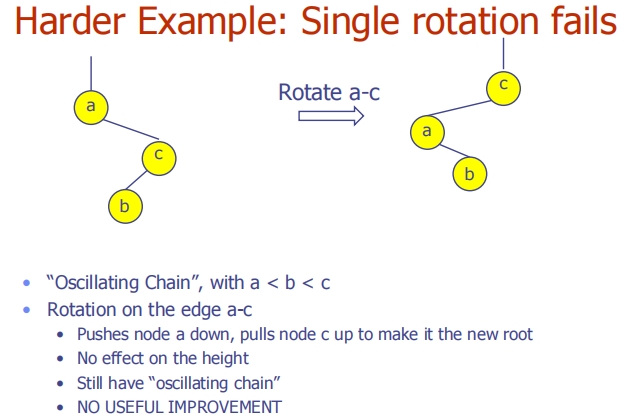
第二张图片 - 更困难的例子：单一旋转失败

• 在这个例子中，树的结构是a作为根，c作为右子节点，而b是c的左子节点，这种结构称为“摆动链”。
• 尝试将c旋转到根位置的单一旋转，并没有实质性地改善树的平衡或减少高度，因为仍然存在一条直线型的结构。
• 这说明单一旋转不总是足够解决平衡问题，特别是在摆动链这种特定配置中。

第三张图片 - 特定例子：双重旋转有效

• 这个例子展示了需要两次旋转才能有效平衡树的情况。
• 首先在b-c边进行旋转，没有立即改变高度，但是调整了b的位置。
• 然后在a-b边进行第二次旋转，将b移至根位置，最终形成了一个平衡的二叉搜索树，有效地减少了高度。
• 这种双重旋转被认为是有时必须的操作，因为单一旋转不能解决所有的平衡问题。

这些图片清楚地演示了在二叉搜索树管理中，如何通过旋转操作来优化树的结构，特别是在面对不同结构配置的树时选择合适的旋转策略。

这张图片描述了在二叉搜索树中使用旋转操作的目的和方法。

主要内容：

1. 旋转的目标：

   • 使用旋转操作的主要目的是控制树的高度，通过减少树的总高度来提高操作的效率。

2. 旋转类型：

   • 单一旋转：有时单一旋转就足以帮助改善树的平衡。
   • 双重旋转：在某些情况下，需要进行双重旋转，即一对协调的单一旋转，以达到更好的平衡效果。

3. 旋转的选择：

   • 在小规模的例子中，可以通过观察直接决定使用哪种旋转。
   • 在一般情况下，需要能够通过算法自动选择合适的旋转，确保每次插入或删除操作后树都能维持或恢复平衡。

应用：

这张图片强调了自平衡二叉搜索树的实际应用，如AVL树和红黑树，这些树种通过内置的旋转规则（算法）自动进行旋转选择，确保了高效的数据操作。这种算法化的旋转选择是现代数据库和内存管理系统中不可或缺的一部分，它允许高效地处理大量动态数据。

这张图片概述了自平衡二叉搜索树（BST）的解决方案和其目标。

自平衡的目标

1. 局部重构：

   • 不断地进行局部结构调整，以响应树中数据的变化（如插入或删除操作）。

2. 保持高度平衡：

   • 确保树的高度保持在对数级别相对于节点的数量，从而使树操作的时间复杂度稳定在 (O(\log n))。

3. 路径限定的旋转：

   • 仅在执行BST操作期间遇到的路径上执行旋转，这样可以减少对整体结构的干扰，并优化旋转的效率。

4. 性能保障：

   • 由于保持了树的高度平衡，树的基本操作（搜索、插入、删除）的性能始终是对数时间的，保证了高效的数据访问和管理。

实现

自平衡树的实现通常涉及一些特定的数据结构，如AVL树和红黑树：

• AVL树：通过在每个节点存储平衡因子（左子树高度与右子树高度的差），并在插入或删除后通过旋转操作维持树的平衡。（不考的）
• 红黑树：通过维持节点颜色的特定规则和在操作过程中调整颜色和进行旋转，确保树的平衡和操作的效率。

这种方法的核心在于通过智能化的结构调整策略，减少维护成本和提高操作性能，使得自平衡二叉搜索树在计算机科学和现代软件工程中广泛应用，特别是在实现数据库和内存管理系统中。

Lecture23 (Shortest Paths: Floyd-Warshall (FW))

这张图片解释了在图论中计算所有点对的最短路径问题及其不同解决方法。

图片内容总结

• 问题定义：寻找图中所有起点和终点节点对的最短路径（SP）。
• Dijkstra 算法：该算法能够找到从单一起始节点到所有其他节点的最短路径。其复杂度为 (O(|V| \log(|V|) + |E|))，其中 (|V|) 是顶点数，(|E|) 是边数。
• 运行 Dijkstra 的方案：可以从每个节点作为起点运行 Dijkstra 算法来解决所有点对最短路径问题，但这样做的复杂度会提高到 (O(|V|^2 \log(|V|) + |V||E|))，因为需要对每个节点重复执行算法。
• Floyd-Warshall 算法：作为一种更适合解决所有点对最短路径问题的算法，Floyd-Warshall 算法将被用于处理，它的时间复杂度为 (O(|V|^3))，适用于处理图中所有节点对的最短路径计算。

解释与应用

• 图中讨论的是解决方案选择：虽然可以通过从每个节点运行 Dijkstra 算法来解决问题，但这种方法在处理大型图时可能效率不高。
• Floyd-Warshall 算法提供了一种时间复杂度稳定的替代方案，尤其适用于顶点数量不是特别大的情况，因为其算法复杂度与图的密度无关，只与节点数量有关。
• 这种方法的优势在于它不仅计算所有顶点对之间的最短路径，还能处理负权边的情况（只要图中没有负权环）。

这张图片有效地概述了在图论算法中针对不同场景选择最合适算法的思考过程，突出了算法效率和适用性的重要性。

这两张图片介绍了Floyd-Warshall（FW）算法在计算所有点对最短路径问题上的应用方法及其数据结构。

第一张图片 - FW算法的基本方法

• 方法类比：FW算法的基本方法与给零钱的方法有相似之处。就像是从一组硬币中建立最佳答案，然后逐个添加硬币的效果一样，FW算法从一组节点开始建立最优解，然后逐个添加其他节点的影响。
• 逐步构建：算法通过使用部分节点集逐步构建最优解，然后一次添加一个节点的影响，最终得到所有节点对的最短路径。

第二张图片 - FW算法的数据结构

• 主数据结构：定义为 d(i, j, k)，表示使用节点集 {1, ..., k} 作为可能的中间节点时，从节点 i 到节点 j 的最短距离。
• 示例解释：例如，d(2, 5, 3) 表示从节点2到节点5，只使用节点 {n1, n2, n3} 作为潜在的中间点的最短距离。
• 节点使用：使用这些中间节点不是强制性的，但不能使用其他未指定的节点，如 n4 等。

FW算法的工作原理

• 初始化：最初，d(i, j, 0) 直接设为节点 i 和 j 之间的边权重（如果存在直接连接的边），否则为无穷大（表示无连接）。
• 迭代更新：对于每个中间节点 k，算法更新所有节点对 (i, j) 的最短距离，考虑通过节点 k 作为中间点是否可以缩短已知的最短路径。更新公式为 d(i, j, k) = min(d(i, j, k-1), d(i, k, k-1) + d(k, j, k-1))。
• 最终结果：完成所有节点的迭代后，d(i, j, n)（其中 n 是节点总数）给出了从节点 i 到节点 j 的最短路径长度。

通过这种方法，FW算法能够有效处理包括负权边的图，但必须保证没有负权回路。这种算法特别适合于节点数量较少的密集图，其中需要频繁查询任意两点间的最短路径。

这张图片描述了在使用Floyd-Warshall算法计算图中所有节点对的最短路径时如何初始化数据结构。

数据结构初始化细节：

• 定义：d(i, j, 0) 表示节点i和节点j之间在不使用任何中间节点的情况下的最佳距离。
• 边的权重：如果节点i和节点j之间存在一条直接的边，那么 d(i, j, 0) 就是这条边的权重 w(i, j)。
• 无直接连接：如果节点i和节点j之间没有直接连接，则 d(i, j, 0) 设为无穷大（Inf），这表示两点之间没有直接路径。

Inf 的实现方式：

• 无穷大（Inf）通常用来表示图中两个节点之间不存在可行路径。
• 在计算机程序中，这可以通过设置一个特殊的值或一个非常大的数字来实现，确保它大于图中任何其他可能的路径长度。

算法的重要性：

• 正确的初始化是Floyd-Warshall算法正确执行的关键，因为它设置了算法的基线，即所有节点对最初的已知最短路径。
• 在算法的后续迭代中，这些初始值将被逐步更新，以考虑通过一个或多个中间节点可能实现的更短路径。

这种初始化方式确保了算法从最简单的情况开始，逐步通过添加中间节点来探索和更新所有可能的路径，从而有效地解决了图中的所有对最短路径问题。

这两张图片详细描述了Floyd-Warshall（FW）算法中添加新节点到已有节点集的迭代过程，并展示了如何更新所有节点对的最短路径。

第一张图片 - 添加第一个中间节点的过程

• 描述：算法现在考虑包括节点 n1 作为可能的中间节点，即 k = 1。
• 路径更新公式：对于任意两个节点 i 和 j，新的最短路径 d(i, j, 1) 是下列两个值中的最小值：
  • 直接从 i 到 j 的距离 d(i, j, 0)（不通过任何中间节点）。
  • 通过节点 n1 的路径长度，即 d(i, n1, 0) + d(n1, j, 0)。

第二张图片 - 添加任意中间节点的一般化过程

• 描述：算法继续迭代，现在考虑包括新的节点 k+1 作为中间节点。
• 路径更新公式：更新公式变得更为一般化，用于任意阶段添加新的中间节点 k+1。新的最短路径 d(i, j, k+1) 是以下两个值中的最小值：
  • 仅使用前 k 个节点作为中间节点的最短路径 d(i, j, k)。
  • 经过新的节点 k+1 的路径长度，即 d(i, k+1, k) + d(k+1, j, k)。

Floyd-Warshall算法的核心原理

• 动态规划：FW算法是一个典型的动态规划问题，它逐步构建解决方案，每一步都基于之前的计算结果。
• 迭代更新：通过逐步引入每一个节点作为潜在的中间节点，算法逐渐找到所有可能的最短路径。
• 全局最优解：通过局部最优的决策（在每一步选择最短的路径），最终达到全局最优的解决方案，即图中任意两点间的最短路径。

这些图片非常有效地说明了FW算法的实现细节和逻辑，这对于理解和应用该算法至关重要，特别是在需要处理复杂网络中多点间交互的场景。

这两张图片进一步详细解释了Floyd-Warshall (FW) 算法的核心方程和它们在动态规划中的应用。

第一张图片 - FW 算法的方程

• 初始化：
  • d(i, j, 0) 是节点 i 到节点 j 的直接距离，如果 i 和 j 之间存在边，则为边的权重 w(i, j)；如果不存在，则为无穷大 Inf。
• 递归更新：
  • d(i, j, k+1) 是在只考虑通过前 k 个节点作为中间节点时，从 i 到 j 的最短路径。这通过比较直接路径 d(i, j, k) 和通过新节点 k+1 的路径 d(i, k+1, k) + d(k+1, j, k) 来更新。

第二张图片 - 关于 k 的注释

• 变量 k 的角色：
  • k 在这里作为一个哑变量，代表了算法考虑的中间节点的数量。方程 d(i, j, k) = min(d(i, j, k-1), d(i, k, k-1) + d(k, j, k-1)) 表示每增加一个中间节点，就尝试更新路径。
• 实际实现时的注意事项：
  • 在实现时，必须注意 k 的取值范围，确保它正确地代表了逐步增加的中间节点。

FW 算法的动态规划应用

• 方程的本质：
  • 这些方程是贝尔曼方程的一种形式，用于动态规划解决最短路径问题。通过递归地解决子问题（较小的 k 值），并在此基础上构建解决更大问题的答案（较大的 k 值）。
• 解决方法：
  • 从 k=0 开始（无中间节点），逐步增加 k，利用之前的计算结果来更新所有节点对 (i, j) 的最短路径长度。

这种方法允许算法不仅计算直接连接的最短路径，还考虑通过一个或多个其他节点的潜在路径，从而提供一种非常强大的方式来处理复杂的图结构，包括那些具有负权边的图（只要不存在负权重环）。

这张图片讨论了在Floyd-Warshall（FW）算法中处理自环（self-edges）的情况，特别是在初始化数据结构时如何定义节点到自身的最短路径距离。

主要内容解释

• 自环的假设：
  • FW算法的标准格式并没有明确指定如何处理节点到其自身的距离，即 d(i, i)。
  • 为了简化计算和保持与Dijkstra算法的一致性，通常会假设从任何节点到它自身的距离为0，即 d(i, i) = 0。这反映了从一个节点到自己不需要任何成本。

为什么这样假设

• 简化计算：
  • 假设 d(i, i) = 0 可以简化FW算法的实现，因为它消除了需要特殊处理节点自环的需求。
• 一致性：
  • 与Dijkstra算法保持一致，后者通常也假设从节点到其自身的距离为0。这样做有助于在理解和应用这两种算法时保持概念上的统一。

实际影响

• 在实际应用中，这种假设意味着算法可以直接在初始化阶段为每个节点的 d(i, i) 赋值为0，无需进一步的条件检查或修改。
• 这也确保了在更新路径距离时，通过自身节点作为中间节点不会产生任何额外成本，因此不会错误地影响其他节点对的最短路径计算。

通过这种方式，Floyd-Warshall算法能够高效地计算图中所有节点对的最短路径，同时避免了在处理自环时可能引入的复杂性或不一致性。

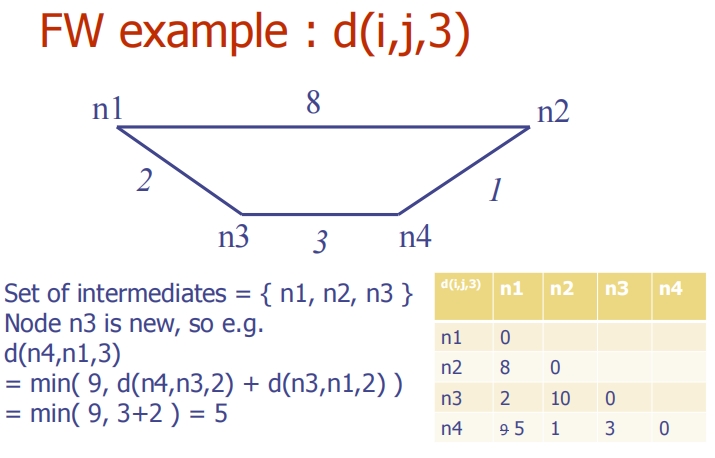
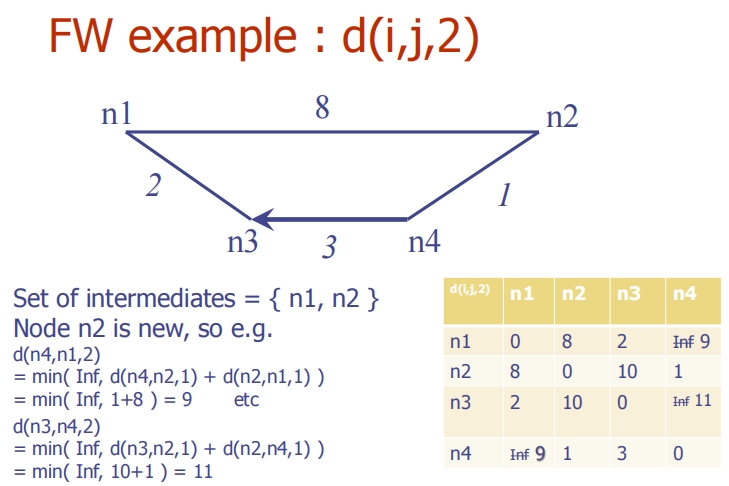
这些图片展示了Floyd-Warshall (FW) 算法在计算所有节点对的最短路径过程中如何逐步添加中间节点并更新距离矩阵。

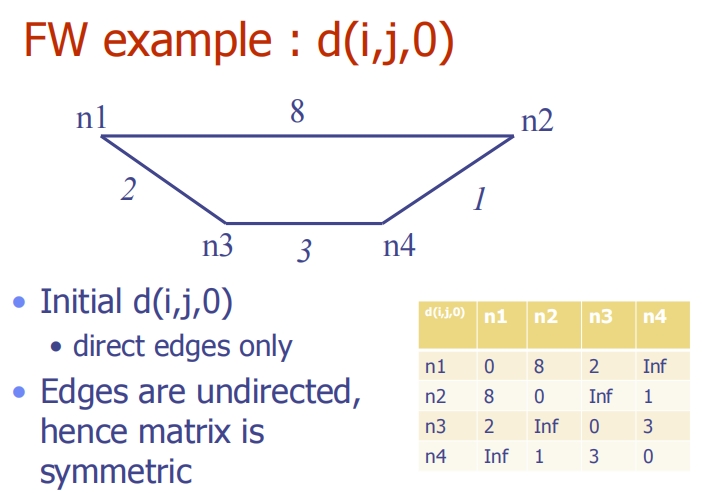
初始阶段：d(i, j, 0)

• 图中节点n1、n2、n3、n4，初始化的距离矩阵 d(i, j, 0) 代表直接边的距离。
• 若节点间有直接边，则填入边的权重，无直接边则填入无穷大（Inf）。
• 例如，n1到n2的直接距离是8，而n3到n2没有直接边，故为Inf。

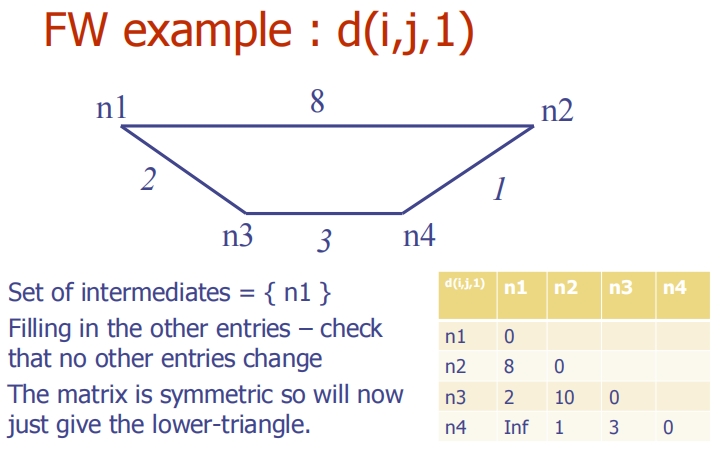
添加第一个中间节点：d(i, j, 1)

• 以n1作为唯一中间节点更新矩阵。
• 更新公式：d(i, j, 1) = min(d(i, j, 0), d(i, n1, 0) + d(n1, j, 0))。
• 例如，d(n3, n2, 1) 是通过n1的路径和直接路径中较短的一个，计算结果为10。

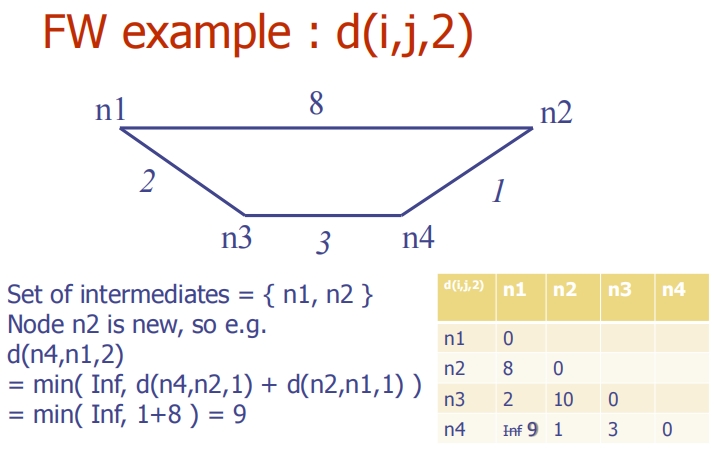
添加第二个中间节点：d(i, j, 2)

• 以n1和n2作为中间节点更新矩阵。
• 更新公式：d(i, j, 2) = min(d(i, j, 1), d(i, n2, 1) + d(n2, j, 1))。
• 例如，d(n4, n1, 2) 更新后为9。

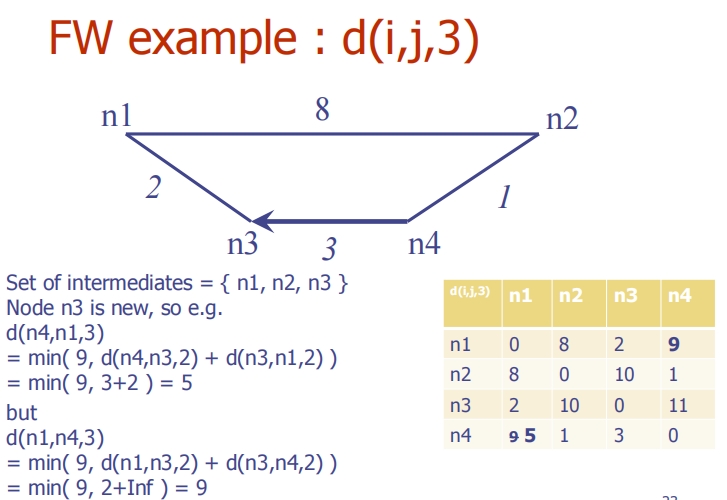
添加第三个中间节点：d(i, j, 3)

• 以n1, n2, 和n3作为中间节点更新矩阵。
• 更新公式：d(i, j, 3) = min(d(i, j, 2), d(i, n3, 2) + d(n3, j, 2))。
• 例如，d(n4, n1, 3) 更新后为5。

最终阶段：d(i, j, 4)

• 以所有节点n1, n2, n3, 和n4作为中间节点。
• 此时的矩阵表示考虑所有节点作为潜在中间节点的最短路径。
• 例如，d(n1, n2, 4) 最终计算结果是通过n4和n3的组合路径长度6，比直接路径8短。

这些示例明确说明了FW算法是如何通过逐步考虑更多的中间节点来优化所有节点对之间的最短路径。这种方法确保了算法能够系统地探索通过可能的所有路径组合，从而找到真正的最短路径。

这张图片介绍了Floyd-Warshall算法的代码结构和其时间复杂度。

主要内容

• 代码结构：

  • 算法的主循环结构包括三个嵌套的循环。外层循环遍历所有可能的中间节点 (k)，中层循环遍历所有起点 (i)，内层循环遍历所有终点 (j)。
  • 更新公式是：d(i, j, k+1) = min(d(i, j, k), d(i, k+1, k) + d(k+1, j, k))，用于计算考虑到中间节点直到 (k+1) 的情况下，从 (i) 到 (j) 的最短路径。

• 复杂度分析：

  • 由于三个循环都遍历整个顶点集 (V)，算法的时间复杂度为 (O(|V|^3))。
  • 这种立方的时间复杂度适用于顶点数量相对较小的密集图。在这种图中，几乎每一对顶点之间都存在边。

• 对比其他算法：

  • 当图是稀疏的，即边的数量 (|E|) 远小于 (|V|^2) 时，使用从每个顶点出发的Dijkstra算法可能更有效，因为Dijkstra算法针对单源最短路径的复杂度通常是 (O(|V| \log |V| + |E|))。

代码实现的注意事项

• 外层循环的重要性：
  • 外层循环 (k) 必须是最外层，因为每次迭代需要在前一次的基础上更新路径长度，确保每次增加的中间节点可以被后续的迭代利用。
• 初始化：
  • 在进入主循环之前，需要正确初始化距离矩阵，为直接连接的节点对设置具体的边权重，未直接连接的设置为无穷大。

这张图片为理解Floyd-Warshall算法的计算过程和其在不同类型的图中应用提供了基础，特别是在分析其效率和适用条件时。

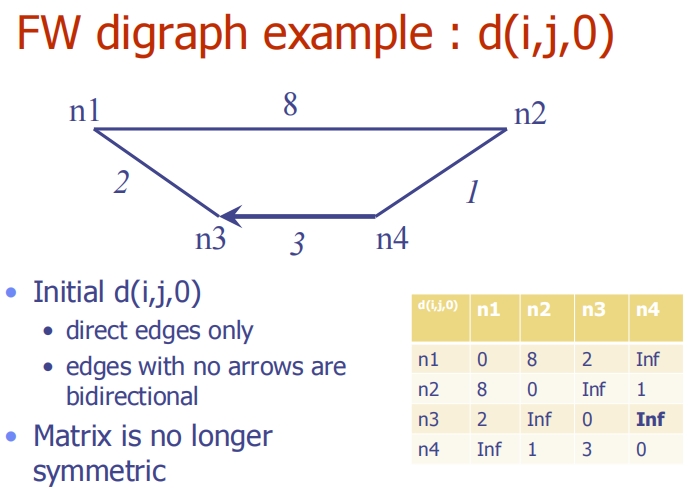
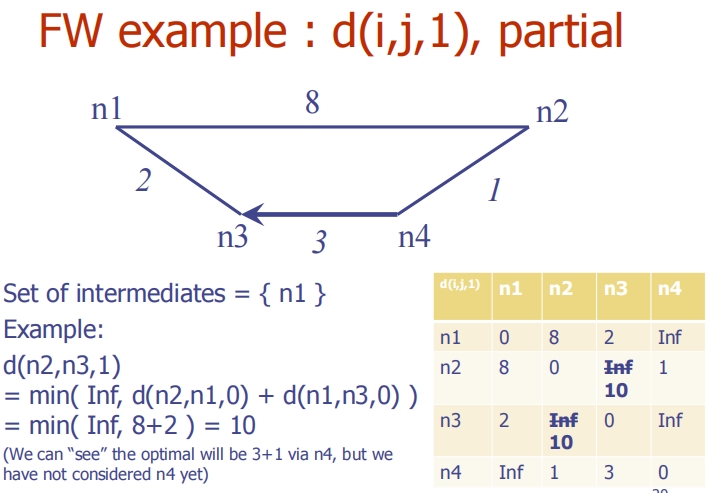
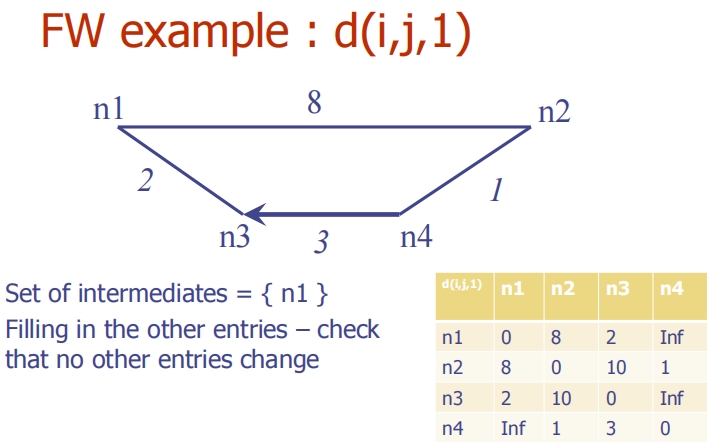
这些图片逐步展示了Floyd-Warshall (FW) 算法在有向图上的应用，具体演示了如何通过逐步增加中间节点来更新所有节点对的最短路径。

初始状态：d(i, j, 0)

• 图中节点包括n1, n2, n3, n4，初始距离矩阵 d(i, j, 0) 只考虑直接的边。
• 每个节点到自己的距离设为0，直接连接的节点显示具体的边权重，未直接连接的节点对的距离设为无穷大。

过程展示：

1. 添加中间节点n1 (d(i, j, 1)):

   • 以n1作为中间节点，更新路径。例如，d(n2, n3, 1) 被更新为通过n1的路径长度8+2=10，因为直接路径不存在（即无穷大）。

2. 添加中间节点n2 (d(i, j, 2)):

   • 加入n2作为中间节点后，继续更新。例如，d(n4, n1, 2) 被更新为通过n2的路径长度1+8=9。

3. 添加中间节点n3 (d(i, j, 3)):

   • 将n3纳入考虑作为中间节点，更新相关路径。例如，d(n4, n1, 3) 更新为通过n3的路径长度3+2=5。

4. 添加中间节点n4 (d(i, j, 4)):

   • 最后添加n4作为中间节点。此时，所有节点都被考虑作为潜在的中间节点。例如，d(n2, n1, 4) 被更新为通过n4的路径长度1+5=6。

总结

每个步骤的计算都基于之前步骤的结果，通过比较直接路径和通过新加入的中间节点的路径长度，选取较小值更新矩阵。这一系列更新逐步优化了矩阵中的值，最终得到各节点对的最短路径。

这些图片清楚地演示了FW算法在处理有向图中如何有效地计算所有节点对的最短路径，同时也说明了算法对于有向和无向图都适用，只是在有向图中，初始的距离矩阵可能不是对称的。这种方法确保了算法能够全面地评估所有可能的路径选择，从而找到最短的路径解决方案。

这张图片介绍了Floyd-Warshall（FW）算法在处理包含负权边的图时的一些关键注意事项。

关键点概述

• 负权边的处理：

  • FW算法能够处理包含负权边的图，这使得它适用于更广泛的场景，比如路由策略、经济模型等领域，其中成本或距离可能会有负值。

• 负权环的问题：

  • 关键的限制是图中不能存在总权重为负的环。这是因为存在负权环会导致算法陷入无限循环，不断通过环路减小路径长度，从而永远无法确定最短路径。

• 示例变更：

  • 提供了一个练习，建议将之前的例子中n4到n3的边权重从+3改为-1，并检查更新后的路径长度计算。这种改变是在没有形成负权环的条件下进行的。

算法的数学基础

• 在没有负权环的条件下，FW算法利用动态规划的方法逐步构建解决方案，每一步都在尝试找到更短的路径。即使存在负权边，只要保证不形成负权环，算法仍然能够有效地计算出所有节点对之间的最短路径。

算法应用的实际意义

• 在实际应用中，如经济学模型、交通流分析等领域，路径的成本可能因为某些策略调整或补贴而出现负值。在这些情况下，能够处理负权值的FW算法特别有用。

结论

通过对FW算法的理解和应用，可以更好地处理复杂网络中的路径优化问题，特别是在涉及复杂成本结构时。此外，这也显示了算法设计时考虑异常或特殊情况的重要性，确保算法的鲁棒性和广泛的适用性。

这张图片回顾了Floyd-Warshall (FW) 算法的核心思想，特别强调了其在动态规划方面的应用。

核心思想概述

• 最短路径的分解性：FW算法利用了最短路径的一个重要特性，即如果一条路径 ( P(A, B) ) 是从点 ( A ) 到点 ( B ) 的最短路径，并且这条路径经过一个中间点 ( M )，那么子路径 ( P(A, M) ) 必须是从 ( A ) 到 ( M ) 的最短路径，同时 ( P(M, B) ) 必须是从 ( M ) 到 ( B ) 的最短路径。

动态规划的应用

• 路径更新：在每一步迭代中，算法都会尝试通过新增的中间节点来更新所有节点对之间的最短路径估计。这个过程反复利用前一步的结果来改进当前步的结果，典型的动态规划方法。
• 递归式的更新：更新公式 ( d(i, j, k+1) = \min(d(i, j, k), d(i, k+1, k) + d(k+1, j, k)) ) 就是基于上述分解性质的动态规划递归式。它表示如果考虑到节点 ( k+1 ) 作为可能的中间点可以获得更短的路径，则更新当前的最短路径估计。

算法设计的深刻洞见

• 通过逐步引入新的中间节点，并基于已有的最短路径信息来更新路径，FW算法展示了如何系统地通过局部最优决策来达到全局最优的复杂问题解决策略。这种方法不仅适用于理论计算，也广泛应用于网络路由优化、社交网络分析、供应链管理等多个领域。

这张图片有效地总结了FW算法的计算机科学基础，特别是它如何巧妙地将图论问题转化为可以通过动态规划有效解决的问题。这种理解对于深入掌握算法设计和分析至关重要。