Untitled

Lecture4

这张幻灯片讨论了特征选择（Feature Selection, FS）和降维（Dimensionality Reduction, DR）的目标。

主要目标包括：

• 减少维度诅咒（Curse of Dimensionality）的影响：在高维数据中，数据稀疏性和计算复杂度增加会导致模型表现不佳。
• 删除冗余特征以提高模型性能：剔除无关或重复的特征可以让模型更加准确和高效。
• 提高计算效率：减少特征数量可以加快训练和预测的速度。
• 降低新数据获取的成本：减少特征数量也可能减少数据收集的复杂性和成本。

特征选择（FS）和降维（DR）的区别：

• 特征选择（FS）：保留原始特征中的一个子集。例如，使用方法如过滤器（Filter）、包装器（Wrapper）或嵌入式方法（Embedded）来选择有用特征。

• 降维（DR）：生成一组新的、更紧凑的特征集合，这些特征可能不保留原始特征的含义。例如，主成分分析（PCA）和线性判别分析（LDA）等方法会将原始特征映射到新的特征空间。

这张幻灯片列出了在使用特征选择（Feature Selection, FS）和降维（Dimensionality Reduction, DR）时需要考虑的因素：

• 目标维度：确定想要减少到的目标特征数量或维度。

• 可解释性：特征选择保留了原始特征，因而通常可解释；而降维生成新的特征，可能无法直接解释。

• 特征相关性/依赖性：需要考虑特征之间的相关性或依赖关系，尤其是在选择或组合特征时。

• 特征的可靠性和重复性：选出的特征或降维后的特征应在不同的数据集或实验中保持一致和可靠。

• 方法：不同的方法可能会选择不同的特征或生成不同的特征。例如，不同的特征选择算法或降维算法可能导致不同的结果。

这张幻灯片介绍了几种常见的特征选择（Feature Selection, FS）方法：

1. 包装方法（Wrapper methods）：

   • 这种方法通过搜索最优的特征子集来最大化模型的决策性能。
   • 常用方法包括递归特征消除（Recursive Feature Elimination）和序列特征选择（Sequential Feature Selection）。

2. 嵌入方法（Embedded methods）：

   • 将特征选择过程集成到模型学习过程中，这意味着特征选择在模型训练时一并完成。
   • 常用方法包括岭回归（Ridge Regression，ElasticNet）、套索回归（Lasso）、随机森林（Random Forest，特征排序）。

3. 过滤方法（Filter-based methods）：

   • 这种方法基于特征之间的关系或统计指标来进行选择，而不是依赖模型性能。
   • 常用方法包括单变量分析（ANOVA）、卡方检验（Chi-Square）、相关性分析和方差分析。

这些方法各有优缺点，选择具体方法时应根据问题的实际情况而定。

这张幻灯片解释了前向特征选择（Forward Feature Selection），这是一种包装方法（Wrapper Method）的一种。前向特征选择通过逐步添加特征来找到最优特征子集。具体步骤如下：

1. 初始设置：

   • ( X \leftarrow \emptyset )：开始时，选定的特征集是空集。

2. 循环直到所有特征都已选择（while ( X \neq F )）：

   • ( B \leftarrow 0 )：初始化最优评估值为0。
   • ( Y \leftarrow \emptyset )：初始化当前选择的特征集为空集。

3. 遍历每个未被选择的特征：

   • 对于每个 ( X_i \in F \setminus X ) （即未选择的特征），将其加入到当前选择的特征集中，并计算新的评估指标 ( M(X \cup {X_i}) )。

4. 更新最优特征集：

   • 如果该评估指标优于当前的最佳指标 ( B )，则更新 ( B ) 和 ( Y )，使 ( Y = X \cup {X_i} )。

5. 判断是否终止：

   • 如果当前的评估指标 ( M(X) ) 大于 ( B )，则终止并返回当前的特征集 ( X )。
   • 否则，更新 ( X \leftarrow Y )，继续循环。

重要变量解释：

• X：最终选择的特征集。
• B：存储的最佳评估指标值。
• Y：每次迭代中选择的特征集。
• M：评估指标，如熵（Entropy）、分类准确率（Classification Rate）或回归误差（Regression Error）。

此外，幻灯片还提到递归特征消除（Recursive Feature Elimination），其过程类似，但从全特征集开始，通过逐步消除特征来达到最优解。

该方法适合寻找能最大化模型性能的特征集，但由于需要多次训练模型，计算成本较高。

这张幻灯片解释了LASSO（最小绝对收缩与选择算子，Least Absolute Shrinkage and Selection Operator），这是一种嵌入式方法（Embedded Method）。

LASSO 的主要特点包括：

• LASSO 添加了一个 L1 正则化项，这个正则化项会惩罚模型中的大权重，从而减少不重要特征的权重。
• 通过这个正则化，LASSO 使得某些特征的权重变为0，从而在实际中减少了有效特征的数量，实现特征选择和降维的效果。

目标函数：

LASSO 的目标是最小化以下损失函数：
[
\min_{x} \left( | Xw - y |^2 + \lambda | w |_1 \right)
]
其中：

• ( | Xw - y |^2 )：最小二乘项，用于拟合模型。
• ( \lambda | w |_1 )：L1正则化项，惩罚特征权重（权重 (w) 的L1范数）。
• ( \lambda ) 是正则化参数，控制特征选择的强度。

正则化参数 ( \lambda ) 的作用：

• 较大的 ( \lambda ) 会使一些特征的权重 ( w ) 变为0，从而减少模型的维度。
• 较小的 ( \lambda ) 则对特征的惩罚较弱，可能会保留更多特征。

例子：

假设有多个特征 ( x_1, x_2, x_3 )，目标是通过调整权重 ( w_1, w_2, w_3 ) 来拟合目标值 ( y )。如果选择较大的 ( \lambda )，某些权重（例如 ( w_2 )）会变为0，这样就可以减少对无用特征 ( x_2 ) 的依赖，进而减少维度。

优化：

由于损失函数中包含L1正则化项，它不可导，因此通常使用次梯度法（Sub-gradient methods）或最小角回归（Least-angle Regression）等方法来优化。

LASSO 的优势在于它不仅可以进行回归分析，还可以有效地减少特征数量，提高模型的可解释性和泛化能力。

这张幻灯片比较了几种用于特征选择的过滤方法（Filter Methods）：卡方检验（Chi-Square）、T检验（T-test）和方差分析（ANOVA），并介绍了这些方法的应用场景。

1. 单变量特征选择（Univariate Feature Selection）：

• 假设各个特征是独立的，分别评估每个特征与目标变量之间的关系。

2. 卡方检验（Chi-Square）：

• 用于检验预测变量（特征）与结果事件（目标变量）之间的独立性。
• 适合处理分类特征和分类目标变量。即用于分类变量之间的关联性测试。

3. T检验（T-test）：

• 比较两个组（通常是二元类）的统计差异。
• 用于连续特征的比较，判断两个组的均值是否有显著差异。

4. 方差分析（ANOVA）：

• 使用方差来测试分类变量与连续结果变量之间的关系。
• 例如，用性别或年龄组来预测考试成绩（连续变量）。

5. 相关性检验（Correlation Test）：

• 用于测试预测变量和结果变量均为连续变量时的相关性。

6. 假设检验（Null-Hypothesis Testing）：

• 这些统计检验基于原假设（即变量之间没有显著关系）。
• 通过计算p值来决定是否拒绝原假设，p值越小，表示越有可能拒绝原假设，通常当p值小于0.01时认为存在显著差异。

总结：

• 卡方检验适合分类变量。
• T检验适合连续变量的二元类比较。
• ANOVA 适合分类变量与连续结果之间的关系分析。
• 相关性检验用于连续变量之间的关系分析。

这张幻灯片介绍了卡方检验（Chi-Square Test）的原理，用于检测分类预测变量与分类结果变量之间的关联性。

主要内容：

• 卡方检验的公式：
  [
  X^2 = \sum \frac{(O - E)^2}{E}
  ]
  其中：

  • ( O ) 是观察到的频率（实际值）。
  • ( E ) 是期望的频率（理论值，根据假设计算的值）。
  • ( \Sigma ) 表示对所有类别求和。

• 原假设（Null Hypothesis）：

  • 卡方检验的原假设是两个分类变量之间相互独立，即它们没有关联性。如果卡方统计量的值较大，表示观察到的频率与期望的频率差异较大，可能拒绝原假设，说明两个变量之间有显著的关联。

图示说明：

• 图表显示了两个分类变量的示例：癌症（Cancer）与非癌症（Noncancer），以及两个特征 ( F1 ) 和 ( F2 ) 的频数分布。
• 通过比较实际观测值与期望值，卡方检验可以判断这两个特征（( F1 ) 和 ( F2 )）是否与癌症或非癌症的分类结果相关。

卡方检验主要用于分类数据的相关性分析，特别是在特征选择过程中，能够帮助识别哪些分类特征对分类目标有显著影响。

这张幻灯片介绍了T检验（T-test），用于比较两个组的均值是否存在显著差异。

主要内容：

• T检验的用途：比较两个组的均值，判断它们是否显著不同。例如，测试癌症组与非癌症组在某个特征值上的差异。

• T检验公式：

  • ( S ) 代表方差的标准误差，计算公式为：
    [
    S = \sqrt{\frac{s^2_{x_1} - s^2_{x_2}}{2}}
    ]
    其中 ( s^2_{x_1} ) 和 ( s^2_{x_2} ) 分别是两组的方差。

  • T统计量的计算公式为：
    [
    t = \frac{\bar{x}_1 - \bar{x}_2}{S \sqrt{\frac{2}{n}}}
    ]
    其中：

    • ( \bar{x}_1 ) 和 ( \bar{x}_2 ) 分别是两组的均值。
    • ( n ) 是样本的数量。

• 图示说明：

  • 图中展示了癌症组（Cancer）和非癌症组（non-Cancer）特征值的分布。两组的均值不同，表现为两条虚线之间的距离。
  • 通过T检验，可以计算出两组均值的差异是否显著。

• 原假设（Null Hypothesis）：

  • 原假设是两组的均值相同，即没有显著差异。如果T统计量足够大，可以拒绝原假设，认为两组均值显著不同。

• p值：

  • T检验的结果通常通过p值来评估。p值越小，表示拒绝原假设的证据越强。当p值低于某个显著性水平（例如0.01或0.05）时，通常认为两个组之间存在显著差异。

总结来说，T检验是用于二元分类特征的均值比较工具，能够判断两个组之间是否存在统计学上的显著差异。

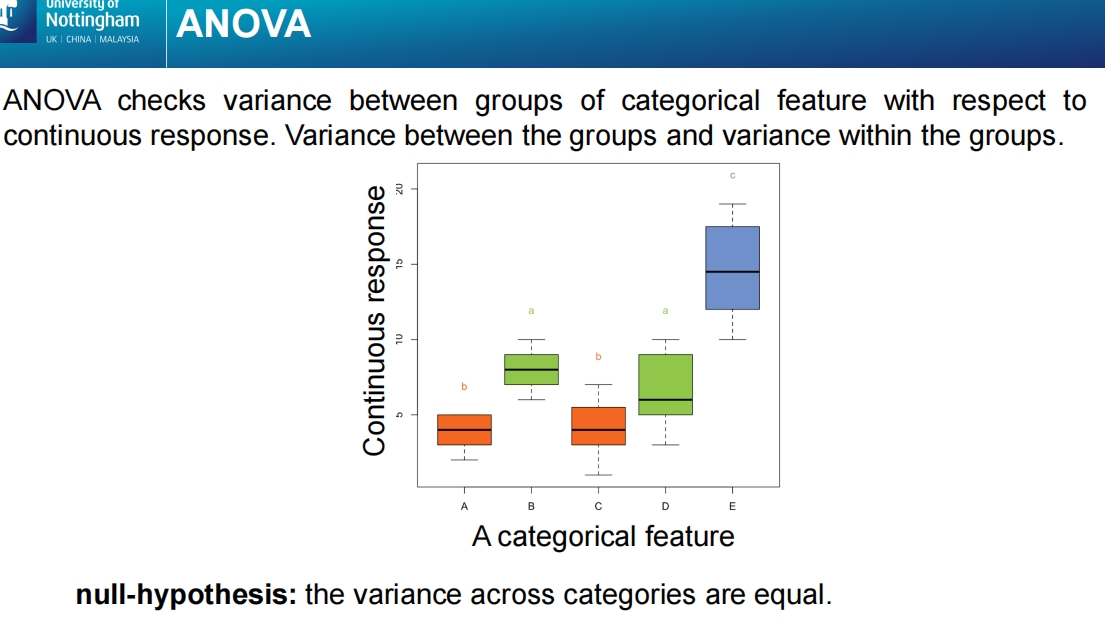
这张幻灯片解释了方差分析（ANOVA，Analysis of Variance）的概念，用于比较分类特征（Categorical Feature）与连续响应变量（Continuous Response）之间的关系。

主要内容：

• ANOVA 检验：方差分析用于检查不同分类组之间的方差是否显著不同。即它比较组间方差和组内方差，判断分类变量（如A、B、C、D、E等）是否对连续变量的结果有显著影响。

• 方差分析的应用：

  • 该方法适用于分类特征（如性别、年龄组等）与连续响应变量（如考试成绩、收入等）之间的关系分析。
  • 通过方差分析可以检验不同组别（如A、B、C、D、E）的连续响应是否存在显著差异。

图示说明：

• 图表展示了五个分类组（A、B、C、D、E）的连续响应值分布（箱线图）。

  • 不同组的方差（数值波动范围）存在差异。例如，E组的响应值分布较高，而A组较低。

• 原假设（Null Hypothesis）：

  • ANOVA 的原假设是：各组之间的方差相等，即各组之间没有显著差异。
  • 如果方差分析结果显示组间方差显著不同，可能拒绝原假设，认为不同组之间存在显著差异。

结论：

ANOVA 是一种强大的工具，用于分析分类特征对连续响应变量的影响，适用于多组间均值的比较。通过检验组间方差，方差分析可以帮助识别哪些分类特征对连续结果有显著影响。

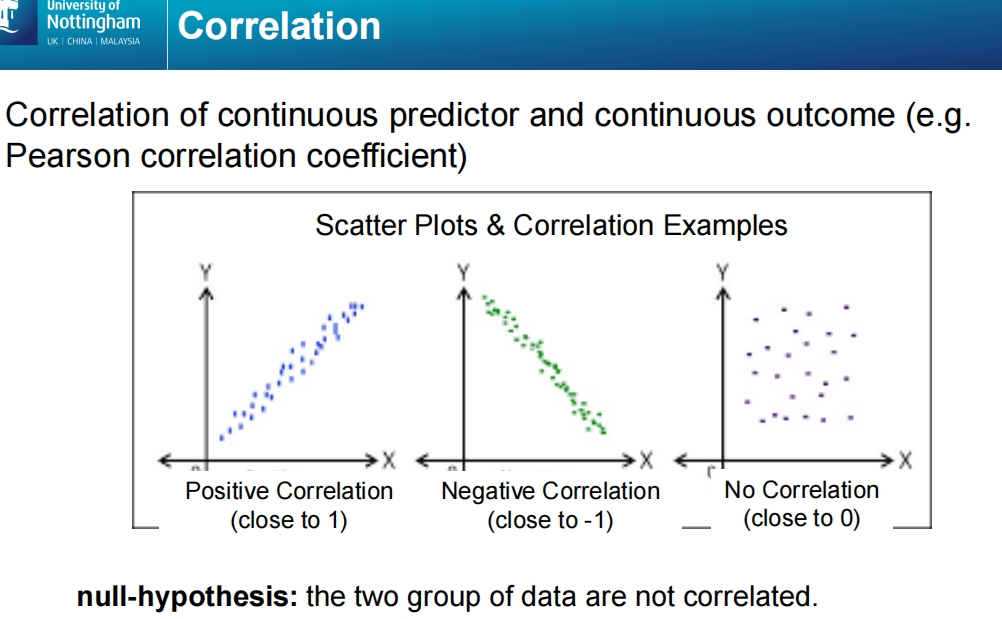
这张幻灯片介绍了相关性分析（Correlation），用于分析连续预测变量与连续结果变量之间的关系，通常使用皮尔逊相关系数（Pearson Correlation Coefficient）来衡量。

主要内容：

• 正相关（Positive Correlation）：

  • 当一个变量增加时，另一个变量也随之增加，称为正相关。
  • 皮尔逊相关系数接近1，表示两者强正相关。图中左侧的散点图展示了一个正相关的例子，数据点大致沿对角线向上排列。

• 负相关（Negative Correlation）：

  • 当一个变量增加时，另一个变量减少，称为负相关。
  • 皮尔逊相关系数接近-1，表示两者强负相关。图中中间的散点图展示了一个负相关的例子，数据点沿对角线向下排列。

• 无相关（No Correlation）：

  • 当两个变量之间没有明显的关系时，称为无相关。
  • 皮尔逊相关系数接近0，表示两者之间没有线性相关性。图中右侧的散点图显示了无相关的例子，数据点分布杂乱无章，没有明显的趋势。

原假设（Null Hypothesis）：

• 相关性检验的原假设是：两个变量之间没有相关性，即它们相互独立。
• 通过相关系数和p值判断是否拒绝原假设。如果相关系数接近1或-1，且p值较低（如p < 0.01），则表明两个变量之间存在显著相关性。

相关性分析是一种常用的统计工具，适用于分析两个连续变量之间的线性关系。

这张幻灯片列举了几种常见的降维方法（Dimensionality Reduction Methods）：

1. 主成分分析（PCA, Principal Component Analysis）：

   • 一种线性降维方法，通过寻找数据中方差最大的方向，将高维数据投影到低维空间。PCA旨在减少维度的同时尽量保留数据的原始信息。
   • 常用于未标记的数据，适合用于探索性数据分析和数据可视化。

2. 线性判别分析（LDA, Linear Discriminant Analysis）：

   • 也是一种线性降维方法，但与PCA不同，LDA是有监督的。它通过最大化类间方差和最小化类内方差来实现降维，主要用于分类任务。
   • 适合用于已标记的数据集，尤其是在分类问题中用于提高分类器的性能。

3. 流形学习（Manifold Learning）：

   • 一种非线性降维方法，旨在保持数据的非线性结构，将高维数据映射到低维空间。流形学习假设数据位于一个嵌入的流形上，因此传统的线性方法如PCA和LDA无法捕捉其复杂性。
   • 常见的流形学习方法包括ISOMAP、t-SNE和局部线性嵌入（LLE）。

这些方法用于应对数据的“维度诅咒”，通过减少数据的维数，提升计算效率并避免过拟合问题。

这张幻灯片介绍了主成分分析（PCA, Principal Component Analysis）的基本计算流程和原理。

主要内容：

1. PCA计算的两种方法：

   • 最大方差法：选择主成分时，PCA寻找的是在新的坐标轴上具有最大方差的方向。
   • 最小化平均投影误差：PCA也可以通过最小化数据点在新轴上的投影误差来进行。

   这两种方法都导向相同的PCA结果，即在保持最多信息的同时减少维度。

2. PCA的计算步骤：

   • 观测变量的均值：首先，计算每个变量的均值，以确保数据集中。
   • 观测变量的协方差矩阵：计算协方差矩阵，描述不同变量之间的线性关系。
   • 特征值和特征向量：通过计算协方差矩阵的特征值和特征向量来确定新的投影轴。特征向量定义了新坐标轴的方向，特征值代表了沿着该轴的方差大小。

3. 特征值和特征向量的计算：

   • 幻灯片提到了一个教学视频链接，介绍如何计算特征向量（Eigenvectors）和特征值（Eigenvalues），这些是PCA的核心部分。

4. 图示说明：

   • 上方的散点图展示了原始特征的二维分布（Feature 1 和 Feature 2），数据呈现一定的线性关系。
   • 下方的散点图展示了PCA之后的结果，数据已经被投影到新特征轴（PCA Feature 1 和 PCA Feature 2）上，维度减少后特征的方差得以最大化。

总结：

PCA通过将高维数据投影到少数几个主要成分上，保留了大部分数据的方差信息，并有效地实现降维。这对于处理高维数据非常有用，能够提高计算效率并减少模型过拟合的风险。

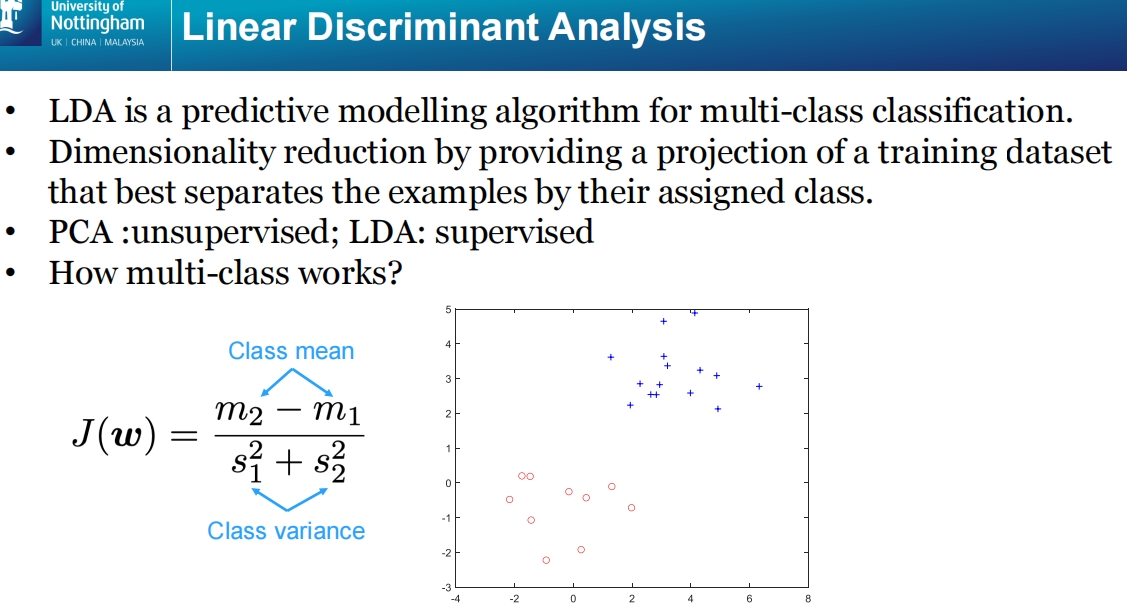
这张幻灯片介绍了线性判别分析（LDA, Linear Discriminant Analysis），用于多分类问题的预测建模和降维。

主要内容：

1. LDA 是一种多分类预测建模算法：

   • LDA 主要用于分类任务，通过投影训练数据集到一个可以最大化类间分离的低维空间，帮助分类器更好地区分不同的类。

2. LDA 的降维功能：

   • LDA 在降维时，通过找到一个能最优分离不同类别的投影方向，将原始高维数据投影到低维空间中。这不仅可以减少维度，还能保留不同类别之间的差异性，帮助分类。

3. 与 PCA 的对比：

   • PCA 是一种无监督学习方法，主要通过最大化方差来实现降维，它不考虑数据类别。
   • LDA 是一种有监督的学习方法，它在降维的同时会考虑数据类别，通过最大化类间方差与最小化类内方差来实现降维和分类。

4. 多分类问题：

   • 在处理多分类任务时，LDA 能够通过计算不同类别的均值和方差，找到最佳的投影方向，从而实现有效的类别区分。

5. 判别准则公式：

   • LDA 的判别准则通过如下公式计算：
     [
     J(w) = \frac{m_2 - m_1}{s_1^2 + s_2^2}
     ]
     其中：
     • ( m_1, m_2 ) 分别是两类的均值。
     • ( s_1^2, s_2^2 ) 分别是两类的方差。
     • 公式的目标是最大化类间均值的差异，同时最小化类内的方差，从而实现最优分类。

6. 图示说明：

   • 图中展示了两个类（红色圈和蓝色十字）的散点分布。通过LDA，数据将被投影到一个可以最优区分这两个类的方向上，从而实现更好的分类效果。

总结：

LDA 是一种有效的降维和分类方法，尤其适用于多分类问题。通过结合类别信息，它能够找到最有利于区分类别的投影方向，减少数据维度的同时提高模型的分类性能。

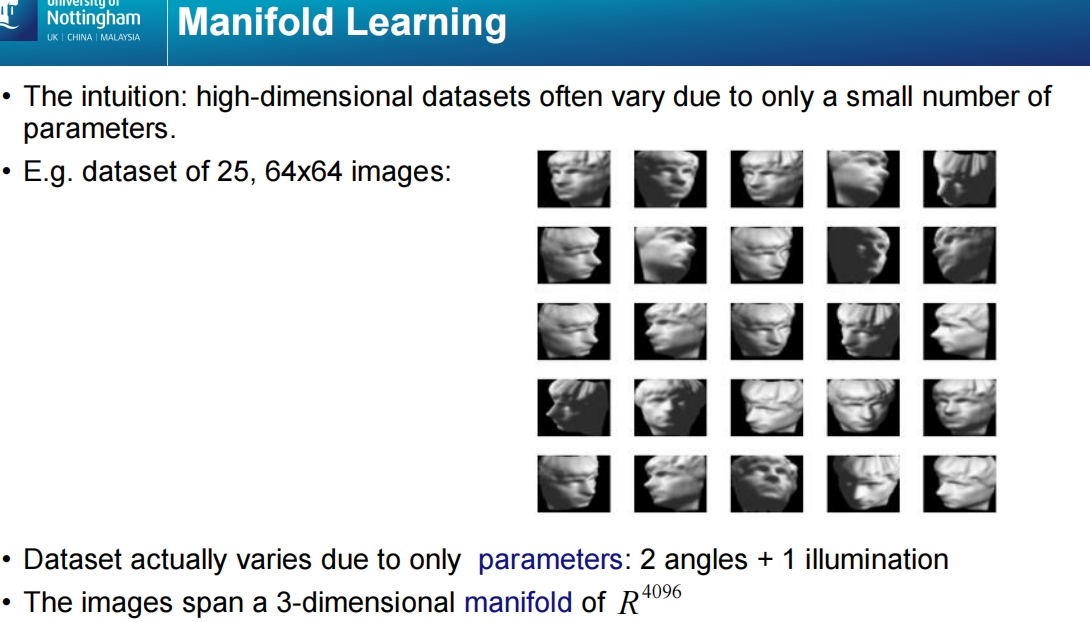
这张幻灯片介绍了流形学习（Manifold Learning）的概念，并通过一个图像数据集的例子来解释其背后的直觉。

主要内容：

1. 流形学习的直觉：

   • 高维数据集通常只由少数几个参数变化控制。尽管数据本身是高维的（例如64x64像素的图像），但这些高维数据实际上可以嵌入到一个低维空间中。
   • 流形学习旨在通过识别数据的低维流形结构来实现降维，捕捉数据中的重要信息。

2. 图像数据集示例：

   • 该示例是一个包含25张64x64像素图像的数据集，每张图像是一个雕像的不同角度或光照条件下的样本。
   • 虽然每张图像是4096维（64x64），但数据集中的变化实际上由少数几个参数控制。

3. 参数变化：

   • 数据集的变化由3个参数决定：
     • 2个角度：雕像的旋转角度。
     • 1个光照条件：光照的方向或强度。
   • 因此，尽管图像是高维的，但数据集的本质变化可以表示为一个3维的流形。

4. 数据的流形表示：

   • 虽然图像存在于4096维的空间中（因为每个图像有4096个像素），但由于数据的变化只由少数参数控制，它们可以被嵌入到一个低维的3维流形中。

结论：

流形学习是一种用于处理高维数据的非线性降维技术，它可以有效地发现和利用数据的低维结构，从而在保留数据核心信息的前提下减少维度。这在图像、文本等高维数据的处理和分析中具有广泛的应用。

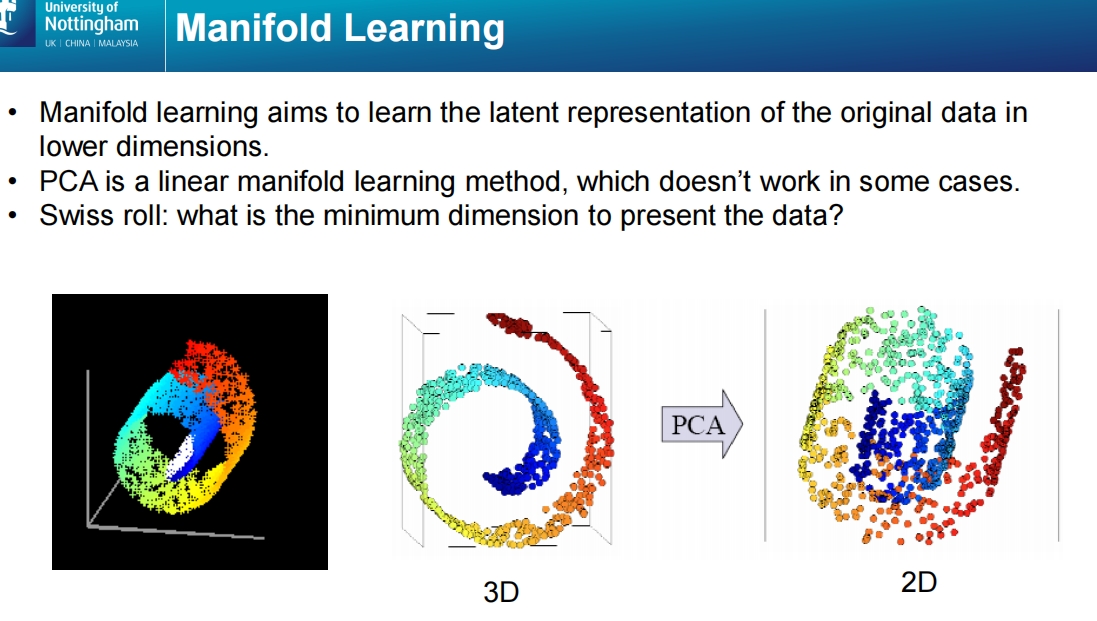
这张幻灯片进一步探讨了流形学习（Manifold Learning），并用Swiss roll（瑞士卷）示例演示了流形学习在处理非线性数据中的作用。

主要内容：

1. 流形学习的目标：

   • 流形学习旨在通过学习原始数据的潜在表示，将数据降维到低维空间中，保留数据的结构和关系。特别是在高维数据中，流形学习能够捕捉数据背后的非线性关系。

2. PCA 和流形学习的对比：

   • PCA 是一种线性降维方法，它假设数据可以通过线性投影来简化。这在处理某些数据时有效，但对于复杂的非线性数据（如Swiss roll），PCA 的效果不佳，因为它不能捕捉数据的非线性结构。
   • 流形学习是一种非线性降维方法，适合用于处理具有复杂几何结构的数据。

3. Swiss roll 示例：

   • 左图展示了一个3维的瑞士卷数据集，数据点呈现出螺旋结构。
   • 中图展示了该数据集的3D表示，通过PCA投影到2D时，无法解开数据的非线性结构。
   • 右图展示了通过合适的非线性流形学习方法将数据成功展开到2D平面上，同时保留了数据点之间的拓扑结构和关系。

4. 最低维度问题：

   • 幻灯片中的问题：“数据的最小维度是什么？” 表明，Swiss roll 的数据实际上可以通过流形学习解开，并映射到二维平面。这表明尽管数据位于高维空间中，其本质上存在于低维的流形中。

总结：

流形学习是一种能够有效处理非线性数据的降维方法。与PCA等线性方法不同，流形学习能够在保持数据局部结构的同时，找到高维数据中的低维流形结构。Swiss roll 示例展示了流形学习在处理复杂几何结构数据中的强大能力。

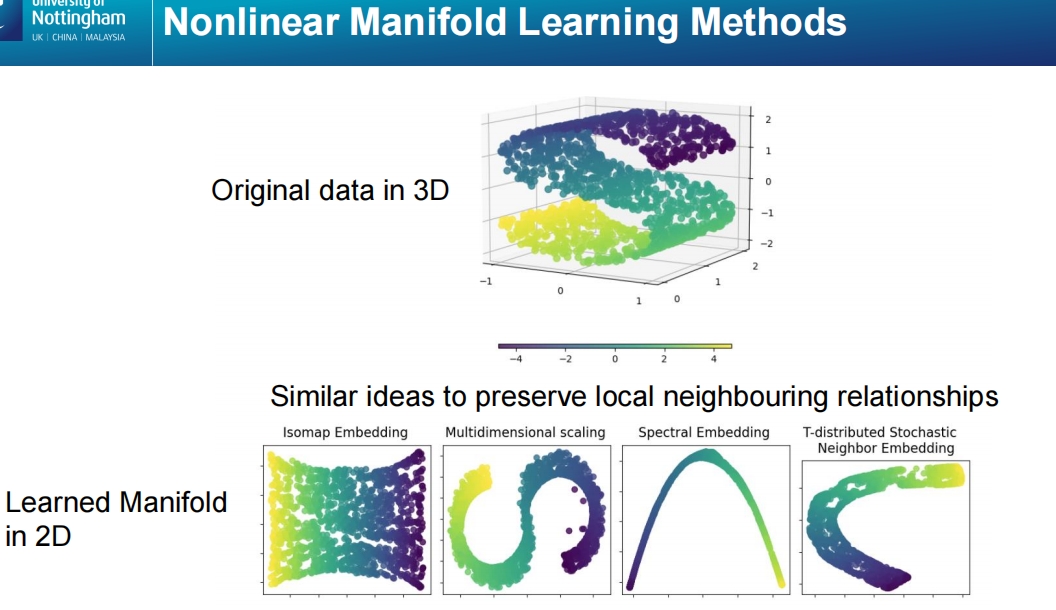
这张幻灯片展示了几种非线性流形学习方法（Nonlinear Manifold Learning Methods），用于从高维数据中学习其低维表示，并强调了这些方法如何保留数据的局部邻域关系。

主要内容：

1. 原始数据的3D表示：

   • 幻灯片顶部的图显示了一个三维数据集，这些数据分布在一个复杂的形状中（类似于卷曲的表面）。
   • 尽管数据存在于高维空间中，但它们的本质结构可以用低维表示来捕捉和描述。

2. 流形学习的目标：

   • 流形学习的目标是通过降维方法，将数据投影到低维空间中，同时保留数据点之间的局部关系。具体来说，它保留了原始高维数据中相邻点之间的几何关系。

3. 常见的非线性流形学习方法：

   • Isomap Embedding：基于测地线距离（即沿流形表面的最短路径）进行降维，有效保留局部结构。
   • 多维尺度法（Multidimensional Scaling, MDS）：通过最小化原始数据点和低维投影点之间的距离差异来实现降维。
   • 谱嵌入（Spectral Embedding）：通过计算图的拉普拉斯矩阵来发现数据的低维流形结构，特别适合处理非线性数据。
   • t-SNE（T-distributed Stochastic Neighbor Embedding）：通过保留高维空间中邻近点的概率分布，在低维空间中重现这种邻近关系，常用于可视化高维数据。

4. 学习后的2D流形表示：

   • 底部的四个图展示了通过上述非线性流形学习方法将数据降维到二维空间的结果。每个方法都能成功地将复杂的高维数据映射到二维空间，同时保留了数据局部邻域之间的关系。
   • 这些方法能够处理PCA等线性方法无法处理的复杂非线性结构，生成的2D表示可以帮助更直观地理解数据的潜在模式和分布。

总结：

非线性流形学习方法能够有效地捕捉和表示高维数据中的复杂非线性结构，并将其映射到低维空间，适用于可视化和分析高维数据中的模式。这些方法在高维数据降维问题上，比线性方法如PCA更具优势，尤其在保留局部邻域关系方面。

这张幻灯片总结了整个内容的关键信息（Key Messages），包括特征选择（FS）、降维（DR）以及相关的流形学习方法的核心知识点。以下是总结的主要内容：

1. 理解特征选择（FS）与降维（DR）的区别：

   • FS（特征选择）是从原始特征中选择一个子集，而 DR（降维）是通过变换来生成新的低维特征。

2. 了解何时使用FS和DR：

   • 在处理高维数据时，选择适当的特征选择或降维方法能够提高模型的性能和效率。

3. 理解关键特征选择方法的工作原理：

   • 学习几种常见的特征选择方法，如过滤方法、嵌入方法和包装方法，了解它们如何根据数据选择最优的特征子集。

4. 理解PCA和LDA的工作原理：

   • PCA（主成分分析）用于无监督学习中的线性降维，LDA（线性判别分析）用于有监督学习中的线性降维和分类。

5. 理解流形学习的概念：

   • 流形学习是一种非线性降维方法，通过寻找高维数据中的低维流形结构，能够更好地表示数据。

6. 了解一些非线性流形学习方法：

   • 掌握几种常用的非线性流形学习方法，如Isomap、MDS、谱嵌入和t-SNE，它们能更好地保留数据局部邻域的几何结构。

总结：

幻灯片的主要目的是让你掌握特征选择和降维的基本原理，并理解何时以及如何使用这些技术，特别是如何选择合适的线性或非线性降维方法来处理复杂的高维数据。